Menu Close

x-2-dx-x-2-x-1-

Tinku Tara 0 Comments
Pin




Question Number 93820 by i jagooll last updated on 15/May/20
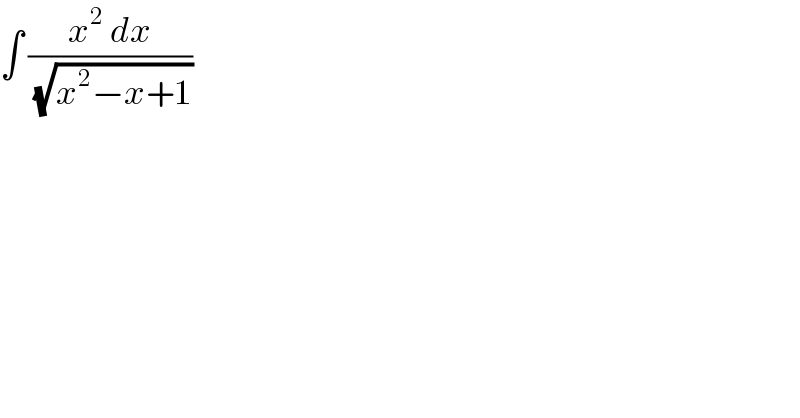
∫ ((x^2 dx)/( (√(x^2 −x+1))))
$$\int\:\frac{{x}^{\mathrm{2}} \:{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\: \\ $$
Commented by mathmax by abdo last updated on 17/May/20
I =∫ (x^2 /( (√(x^2 −x+1))))dx ⇒I =∫ ((x^2 −x+1)/( (√(x^2 −x+1))))dx +∫ ((x−1)/( (√(x^2 −x+1))))dx=I_1 +I_2 ∫ ((x^2 −x+1)/( (√(x^2 −x+1))))dx =∫(√(x^2 −x+1))dx =∫ (√((x−(1/2))^2 +(3/4)))dx =_(x−(1/2)=((√3)/2)sh(t)) ((√3)/2) ∫ ch(t)×((√3)/2) ch(t)dt =(3/4)∫(((1+ch(2t))/2))dt =(3/8) t +(3/(16))sh(2t) +c =(3/8)t +(3/8)sh(t)ch(t) +c =(3/8) argsh(((2x−1)/( (√3))))+(3/8)(((2x−1)/3))(√(1+(((2x−1)/( (√3))))^2 )) I_2 =(1/2)∫((2x−1−1)/( (√(x^2 −x+1)))) dx =(√(x^2 −x+1)) −(1/2) ∫ (dx/( (√(x^2 −x+1)))) ∫ (dx/( (√(x^2 −x+1)))) =_(x−(1/2)=((√3)/2)t) ((√3)/2) ∫ (dt/(((√3)/2)(√(1+t^2 )))) =∫ (dt/( (√(1+t^2 )))) =ln(t+(√(1+t^2 ))) =ln(((2x−1)/( (√3)))+(√(1+(((2x−1)/( (√3) )))^2 ))) ⇒ I =(3/8)ln(((2x−1)/( (√3)))+(√(1+(((2x−1)/( (√3))))^2 ))) +((2x−1)/8)(√(1+(((2x−1)/( (√3))))^2 )) +(√(x^2 −x+1))−(1/2)ln(((2x−1)/( (√3)))+(√(1+(((2x−1)/( (√3))))^2 ))) +C =−(1/8)ln(((2x−1)/( (√3)))+(√(1+(((2x−1)/( (√3))))^2 )))+(√(x^2 −x+1))+((2x−1)/8)(√(1+(((2x−1)/( (√3))))^2 ))+C
$${I}\:=\int\:\:\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}\:\Rightarrow{I}\:=\int\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}\:+\int\:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}={I}_{\mathrm{1}} \:+{I}_{\mathrm{2}} \\ $$$$\int\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}\:=\int\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:=\int\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dx} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)} \:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int\:{ch}\left({t}\right)×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{ch}\left({t}\right){dt}\:=\frac{\mathrm{3}}{\mathrm{4}}\int\left(\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\:{t}\:\:+\frac{\mathrm{3}}{\mathrm{16}}{sh}\left(\mathrm{2}{t}\right)\:+{c}\:=\frac{\mathrm{3}}{\mathrm{8}}{t}\:+\frac{\mathrm{3}}{\mathrm{8}}{sh}\left({t}\right){ch}\left({t}\right)\:+{c} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\:{argsh}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{3}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\:{dx}\:=\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$$\int\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int\:\:\frac{{dt}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:=\int\:\frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:={ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$={ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}\right)^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{3}}{\mathrm{8}}{ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{8}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)\:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{8}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }+{C} \\ $$
Answered by Kunal12588 last updated on 15/May/20
I=∫((x^2 dx)/( (√(x^2 −x+1)))) =∫((x^2 −x+1)/( (√(x^2 −x+1))))dx+∫((x−1)/( (√(x^2 −x+1))))dx =∫(√(x^2 −x+1)) dx + (1/2)∫((2x−1)/( (√(x^2 −x+1))))dx−(1/2)∫(dx/( (√(x^2 −x+1)))) =∫(√((x−(1/2))^2 +(((√3)/2))^2 )) dx + (1/2)∫((d(x^2 −x+1))/( (√(x^2 −x+1)))) −(1/2)∫(dx/( (√((x−(1/2))+(((√3)/2))^2 )))) =(1/2)(x−(1/2))(√(x^2 −x+1))+(3/8)ln∣x−(1/2)+(√(x^2 −x+1))∣ +(1/2)×2(√(x^2 −x+1))−(1/2)×(2/( (√3))) tan^(−1) ((2x−1)/( (√3)))+C =(1/4)(2x−1)(√(x^2 −x+1))+(3/8)ln∣x−(1/2)+(√(x^2 −x+1))∣ +(√(x^2 −x+1))−(1/( (√3)))tan^(−1) ((2x−1)/( (√3)))+C =(1/4)(2x+3)(√(x^2 −x+1))+(3/8)ln∣x−(1/2)+(√(x^2 −x+1))∣ −(1/( (√3)))tan^(−1) ((2x−1)/( (√3)))+C
$${I}=\int\frac{{x}^{\mathrm{2}} {dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$$=\int\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}+\int\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx} \\ $$$$=\int\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$$=\int\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mid{x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid \\ $$$$\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mid{x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid \\ $$$$\:\:\:\:+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{8}}{ln}\mid{x}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$
Commented by i jagooll last updated on 15/May/20
waw..great sir
$$\mathrm{waw}..\mathrm{great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *