Question Number 157655 by tounghoungko last updated on 26/Oct/21
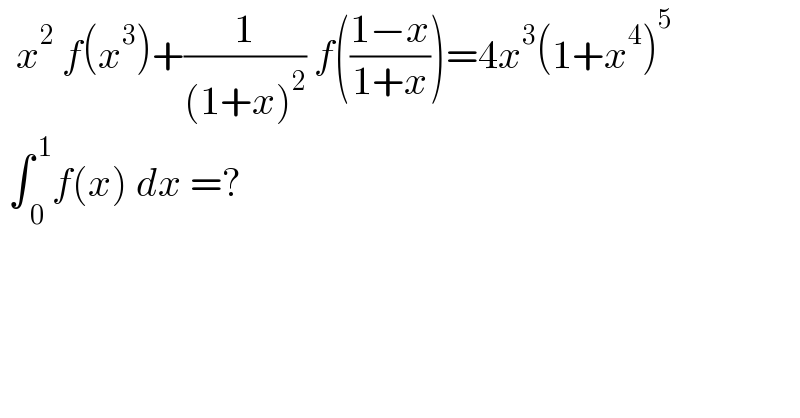
$$\:\:{x}^{\mathrm{2}} \:{f}\left({x}^{\mathrm{3}} \right)+\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\:{f}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)=\mathrm{4}{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{4}} \right)^{\mathrm{5}} \\ $$$$\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} {f}\left({x}\right)\:{dx}\:=? \\ $$
Commented by cortano last updated on 26/Oct/21

$$=\:\frac{\mathrm{65}}{\mathrm{3}} \\ $$
Answered by mindispower last updated on 26/Oct/21
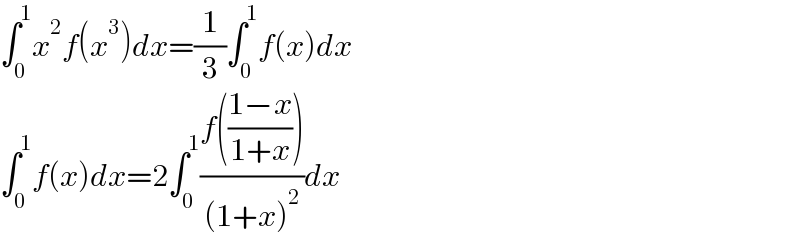
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {f}\left({x}^{\mathrm{3}} \right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{f}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx} \\ $$
