Question Number 83786 by jagoll last updated on 06/Mar/20
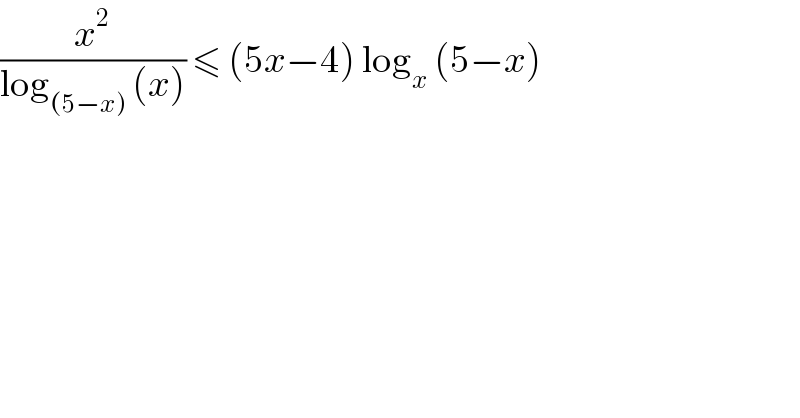
$$\frac{{x}^{\mathrm{2}} }{\mathrm{log}_{\left(\mathrm{5}−{x}\right)} \:\left({x}\right)}\:\leqslant\:\left(\mathrm{5}{x}−\mathrm{4}\right)\:\mathrm{log}_{{x}} \:\left(\mathrm{5}−{x}\right)\: \\ $$
Answered by john santu last updated on 06/Mar/20
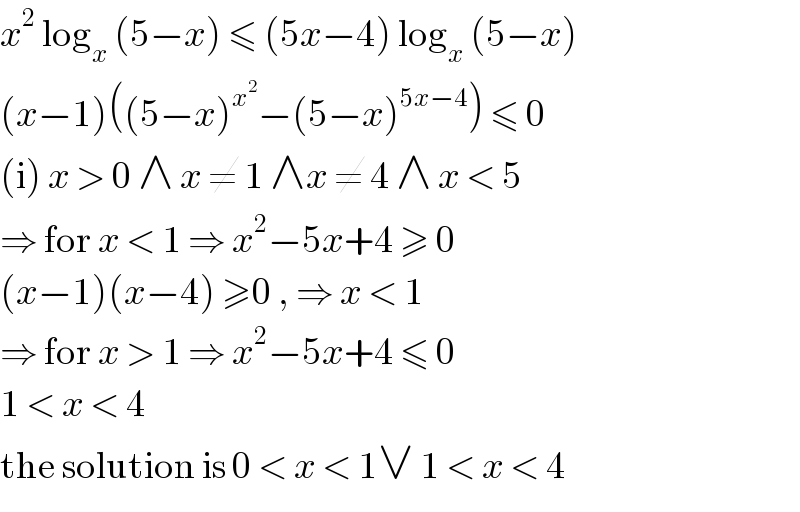
$${x}^{\mathrm{2}} \:\mathrm{log}_{{x}} \:\left(\mathrm{5}−{x}\right)\:\leqslant\:\left(\mathrm{5}{x}−\mathrm{4}\right)\:\mathrm{log}_{{x}} \:\left(\mathrm{5}−{x}\right) \\ $$$$\left({x}−\mathrm{1}\right)\left(\left(\mathrm{5}−{x}\right)^{{x}^{\mathrm{2}} } −\left(\mathrm{5}−{x}\right)^{\mathrm{5}{x}−\mathrm{4}} \right)\:\leqslant\:\mathrm{0} \\ $$$$\left(\mathrm{i}\right)\:{x}\:>\:\mathrm{0}\:\wedge\:{x}\:\neq\:\mathrm{1}\:\wedge{x}\:\neq\:\mathrm{4}\:\wedge\:{x}\:<\:\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{for}\:{x}\:<\:\mathrm{1}\:\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\:\geqslant\:\mathrm{0}\: \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)\:\geqslant\mathrm{0}\:,\:\Rightarrow\:{x}\:<\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{for}\:{x}\:>\:\mathrm{1}\:\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\:\leqslant\:\mathrm{0} \\ $$$$\mathrm{1}\:<\:{x}\:<\:\mathrm{4} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{0}\:<\:{x}\:<\:\mathrm{1}\vee\:\mathrm{1}\:<\:{x}\:<\:\mathrm{4} \\ $$
Commented by jagoll last updated on 06/Mar/20
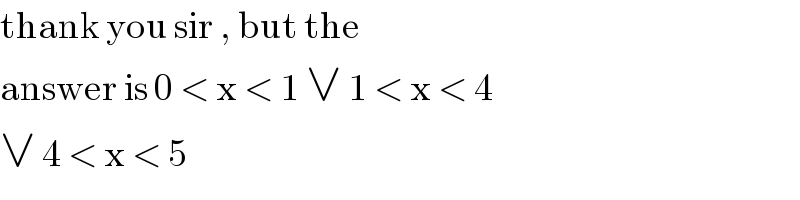
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:,\:\mathrm{but}\:\mathrm{the}\: \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{0}\:<\:\mathrm{x}\:<\:\mathrm{1}\:\vee\:\mathrm{1}\:<\:\mathrm{x}\:<\:\mathrm{4}\: \\ $$$$\vee\:\mathrm{4}\:<\:\mathrm{x}\:<\:\mathrm{5} \\ $$
Answered by MJS last updated on 07/Mar/20
![x^2 ((ln (5−x))/(ln x))≤(5x−4)((ln (5−x))/(ln x)) 0<x<5 ∧ x≠1 ∧ x≠4 case 1 ((ln (5−x))/(ln x))>0 ∧ x^2 ≤5x−4 case 1.1 ln (5−x) <0 ∧ ln x <0 no solution case 1.2 ln (5−x) >0 ∧ ln x >0 1<x<4 x^2 −5x+4≤0 ⇒ 1≤x≤5 ⇒ 1<x<4 case 2 ((ln (5−x))/(ln x))<0 ∧ x^2 ≥5x−4 case 2.1 ln (5−x) <0 ∧ ln x >0 4<x<5 case 2.2 ln (5−x) >0 ∧ ln x <0 0<x<1 x^2 −5x+4≥0 ⇒ x≤1 ∨ x≥4 ⇒ 0<x<1 ∨ 4<x<5 answer x∈]0; 5[\{1; 4} but regarding the limits we could define for 0≤x≤5](https://www.tinkutara.com/question/Q83916.png)
$${x}^{\mathrm{2}} \frac{\mathrm{ln}\:\left(\mathrm{5}−{x}\right)}{\mathrm{ln}\:{x}}\leqslant\left(\mathrm{5}{x}−\mathrm{4}\right)\frac{\mathrm{ln}\:\left(\mathrm{5}−{x}\right)}{\mathrm{ln}\:{x}} \\ $$$$\mathrm{0}<{x}<\mathrm{5}\:\wedge\:{x}\neq\mathrm{1}\:\wedge\:{x}\neq\mathrm{4} \\ $$$$\mathrm{case}\:\mathrm{1}\:\frac{\mathrm{ln}\:\left(\mathrm{5}−{x}\right)}{\mathrm{ln}\:{x}}>\mathrm{0}\:\wedge\:{x}^{\mathrm{2}} \leqslant\mathrm{5}{x}−\mathrm{4} \\ $$$$\:\:\:\:\:\mathrm{case}\:\mathrm{1}.\mathrm{1}\:\mathrm{ln}\:\left(\mathrm{5}−{x}\right)\:<\mathrm{0}\:\wedge\:\mathrm{ln}\:{x}\:<\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{no}\:\mathrm{solution} \\ $$$$\:\:\:\:\:\mathrm{case}\:\mathrm{1}.\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{5}−{x}\right)\:>\mathrm{0}\:\wedge\:\mathrm{ln}\:{x}\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{1}<{x}<\mathrm{4} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\leqslant\mathrm{0}\:\Rightarrow\:\mathrm{1}\leqslant{x}\leqslant\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{1}<{x}<\mathrm{4} \\ $$$$\mathrm{case}\:\mathrm{2}\:\frac{\mathrm{ln}\:\left(\mathrm{5}−{x}\right)}{\mathrm{ln}\:{x}}<\mathrm{0}\:\wedge\:{x}^{\mathrm{2}} \geqslant\mathrm{5}{x}−\mathrm{4} \\ $$$$\:\:\:\:\:\mathrm{case}\:\mathrm{2}.\mathrm{1}\:\mathrm{ln}\:\left(\mathrm{5}−{x}\right)\:<\mathrm{0}\:\wedge\:\mathrm{ln}\:{x}\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{4}<{x}<\mathrm{5} \\ $$$$\:\:\:\:\:\mathrm{case}\:\mathrm{2}.\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{5}−{x}\right)\:>\mathrm{0}\:\wedge\:\mathrm{ln}\:{x}\:<\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\geqslant\mathrm{0}\:\Rightarrow\:{x}\leqslant\mathrm{1}\:\vee\:{x}\geqslant\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{0}<{x}<\mathrm{1}\:\vee\:\mathrm{4}<{x}<\mathrm{5} \\ $$$$ \\ $$$$\left.\mathrm{answer}\:{x}\in\right]\mathrm{0};\:\mathrm{5}\left[\backslash\left\{\mathrm{1};\:\mathrm{4}\right\}\right. \\ $$$$\mathrm{but}\:\mathrm{regarding}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{we}\:\mathrm{could}\:\mathrm{define}\:\mathrm{for} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{5} \\ $$
