Question Number 17167 by Arnab Maiti last updated on 01/Jul/17

$$\int\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \mathrm{3x}\:\mathrm{dx} \\ $$
Answered by sma3l2996 last updated on 01/Jul/17
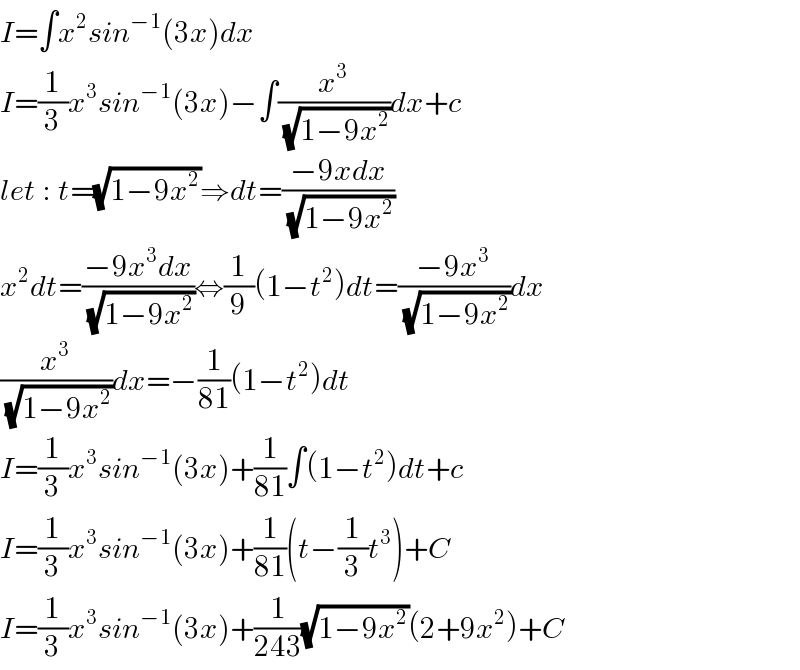
$${I}=\int{x}^{\mathrm{2}} {sin}^{−\mathrm{1}} \left(\mathrm{3}{x}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {sin}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)−\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }}{dx}+{c} \\ $$$${let}\::\:{t}=\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }\Rightarrow{dt}=\frac{−\mathrm{9}{xdx}}{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }} \\ $$$${x}^{\mathrm{2}} {dt}=\frac{−\mathrm{9}{x}^{\mathrm{3}} {dx}}{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }}\Leftrightarrow\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}=\frac{−\mathrm{9}{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }}{dx}=−\frac{\mathrm{1}}{\mathrm{81}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {sin}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)+\frac{\mathrm{1}}{\mathrm{81}}\int\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}+{c} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {sin}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)+\frac{\mathrm{1}}{\mathrm{81}}\left({t}−\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} \right)+{C} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} {sin}^{−\mathrm{1}} \left(\mathrm{3}{x}\right)+\frac{\mathrm{1}}{\mathrm{243}}\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} }\left(\mathrm{2}+\mathrm{9}{x}^{\mathrm{2}} \right)+{C} \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17

$$\mathcal{T}\mathfrak{hank}\:\mathfrak{you}\:\mathfrak{very}\:\mathfrak{much}. \\ $$
