Question Number 187529 by sciencestudentW last updated on 18/Feb/23
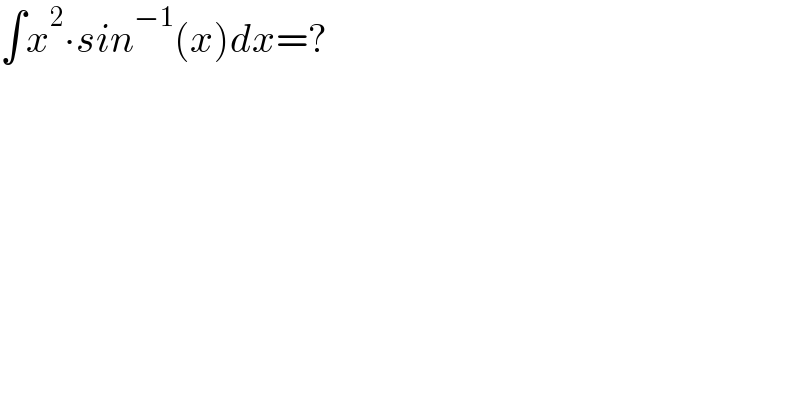
$$\int{x}^{\mathrm{2}} \centerdot{sin}^{−\mathrm{1}} \left({x}\right){dx}=? \\ $$
Answered by Humble last updated on 18/Feb/23
![∫x^2 arcsin(x)dx IBP =(1/3)x^3 arcsin(x)−∫(x^3 /(3(√(1−x^2 ))))dx ∫(x^3 /(3(√(1−x^2 ))))dx = (1/3)[(1/3)(−x^2 )^(3/2) −(√(1−x^2 ))] =(1/3)arcsin(x)−(1/3)[(1/3)(1−x^2 )^(3/2) −(√(1−x^2 ))]+C](https://www.tinkutara.com/question/Q187540.png)
$$\int\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{arcsin}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{I}}{BP} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{x}}^{\mathrm{3}} \boldsymbol{{arcsin}}\left(\boldsymbol{{x}}\right)−\int\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\boldsymbol{{dx}} \\ $$$$\int\frac{\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{3}\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\boldsymbol{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\mathrm{3}}\left(−\boldsymbol{{x}}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{arcsin}}\left(\boldsymbol{{x}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right]+\boldsymbol{{C}} \\ $$
