Question Number 105753 by bramlex last updated on 31/Jul/20
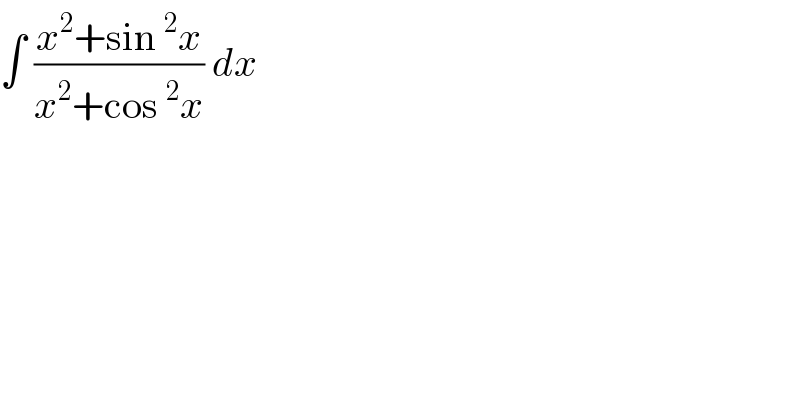
$$\int\:\frac{{x}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$
Commented by Ar Brandon last updated on 31/Jul/20

$$\mathrm{No}\:\mathrm{limits}\:? \\ $$
Answered by bobhans last updated on 31/Jul/20
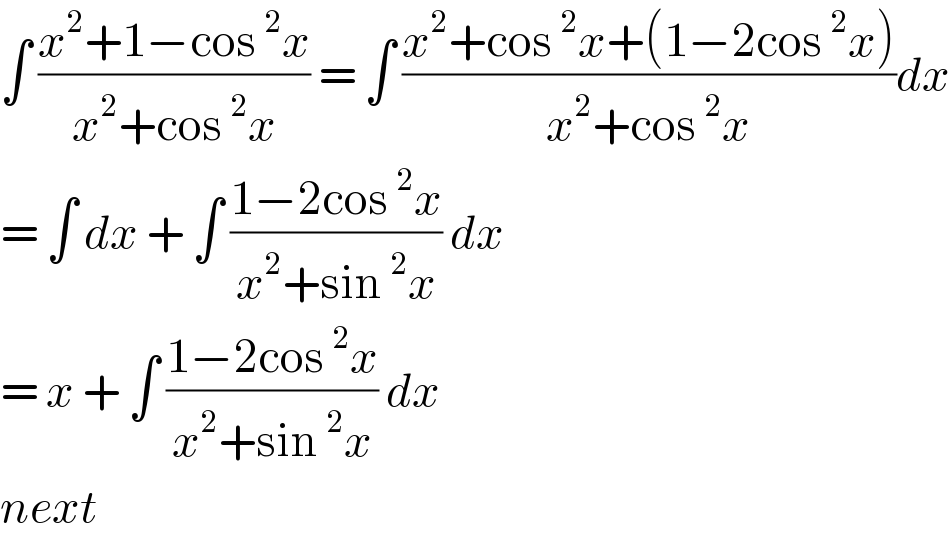
$$\int\:\frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{cos}\:^{\mathrm{2}} {x}}\:=\:\int\:\frac{{x}^{\mathrm{2}} +\mathrm{cos}\:^{\mathrm{2}} {x}+\left(\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} {x}\right)}{{x}^{\mathrm{2}} +\mathrm{cos}\:^{\mathrm{2}} {x}}{dx} \\ $$$$=\:\int\:{dx}\:+\:\int\:\frac{\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$$$=\:{x}\:+\:\int\:\frac{\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +\mathrm{sin}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$$${next} \\ $$
