Question Number 96911 by Ar Brandon last updated on 05/Jun/20
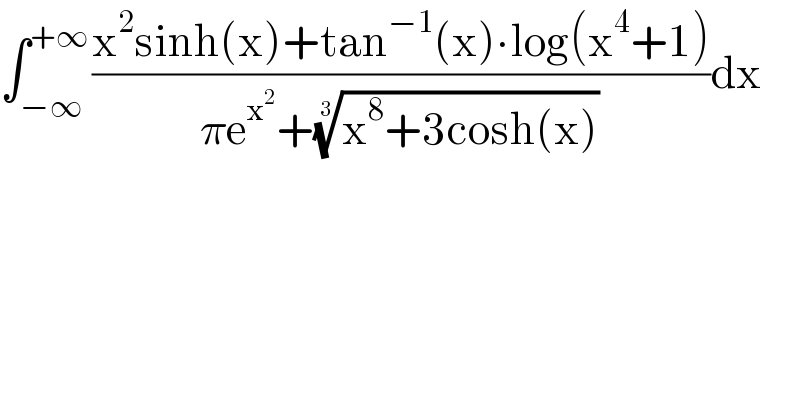
$$\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{sinh}\left(\mathrm{x}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\centerdot\mathrm{log}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}{\pi\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{8}} +\mathrm{3cosh}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$
Commented by 675480065 last updated on 05/Jun/20

$$=\mathrm{0}\: \\ $$
Commented by Ar Brandon last updated on 05/Jun/20
cool ��
Answered by Ar Brandon last updated on 05/Jun/20
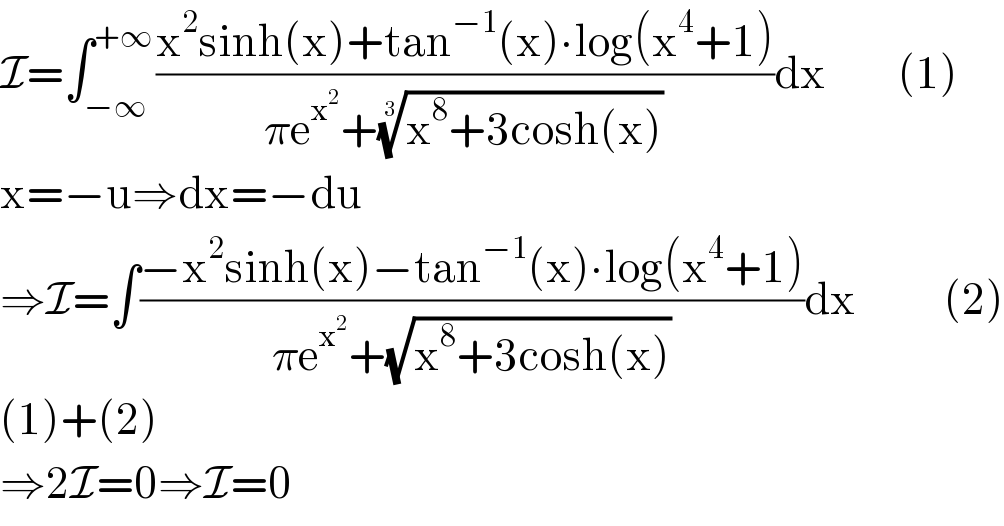
$$\mathcal{I}=\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{sinh}\left(\mathrm{x}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\centerdot\mathrm{log}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}{\pi\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\sqrt[{\mathrm{3}}]{\mathrm{x}^{\mathrm{8}} +\mathrm{3cosh}\left(\mathrm{x}\right)}}\mathrm{dx}\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{x}=−\mathrm{u}\Rightarrow\mathrm{dx}=−\mathrm{du} \\ $$$$\Rightarrow\mathcal{I}=\int\frac{−\mathrm{x}^{\mathrm{2}} \mathrm{sinh}\left(\mathrm{x}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\centerdot\mathrm{log}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)}{\pi\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\sqrt{\mathrm{x}^{\mathrm{8}} +\mathrm{3cosh}\left(\mathrm{x}\right)}}\mathrm{dx}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{2}\mathcal{I}=\mathrm{0}\Rightarrow\mathcal{I}=\mathrm{0} \\ $$
