Menu Close

x-2-x-1-x-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 154621 by liberty last updated on 20/Sep/21
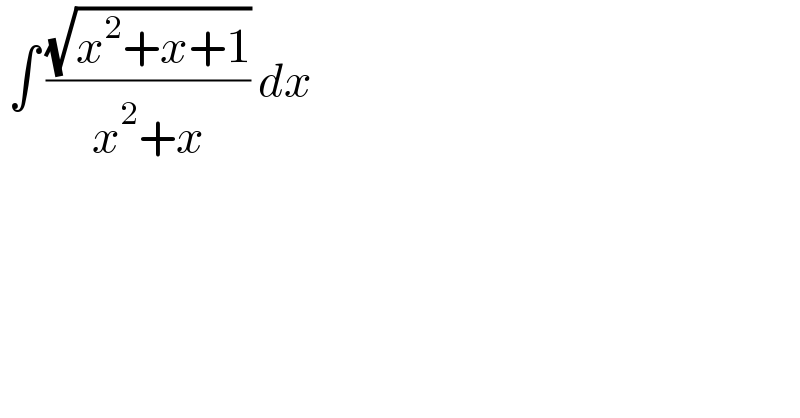
∫ ((√(x^2 +x+1))/(x^2 +x)) dx
$$\:\int\:\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{\mathrm{2}} +{x}}\:{dx}\: \\ $$
Commented by mathdanisur last updated on 20/Sep/21
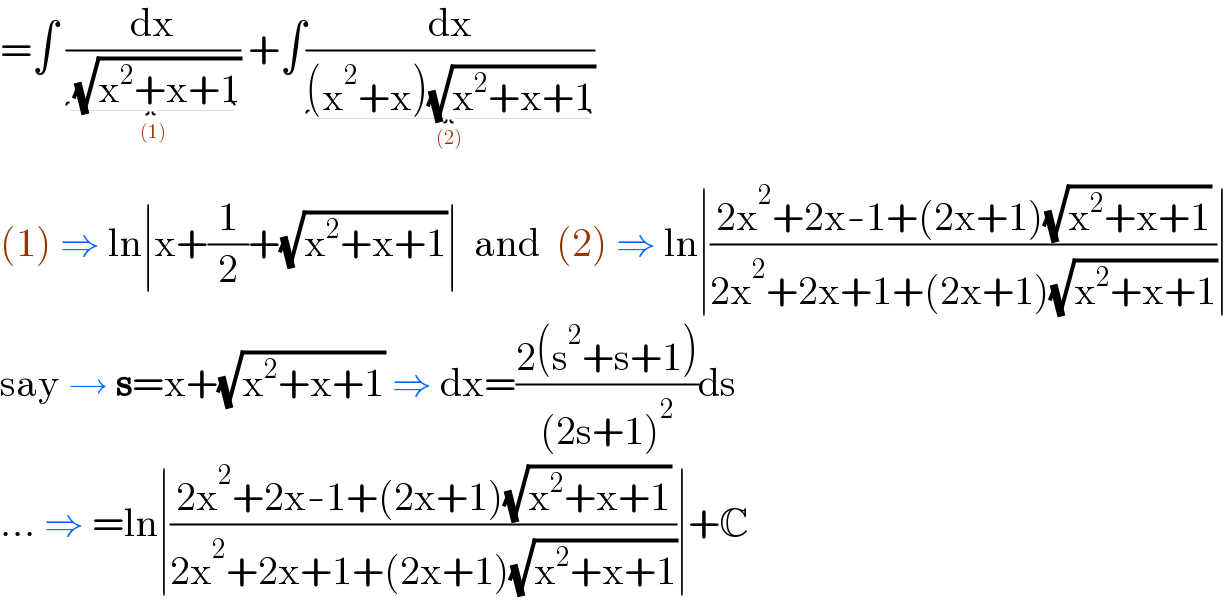
=∫ (dx/( (√(x^2 +x+1))))_() +∫(dx/((x^2 +x)(√(x^2 +x+1))))_() (1) ⇒ ln∣x+(1/2)+(√(x^2 +x+1))∣ and (2) ⇒ ln∣((2x^2 +2x-1+(2x+1)(√(x^2 +x+1)))/(2x^2 +2x+1+(2x+1)(√(x^2 +x+1))))∣ say → s=x+(√(x^2 +x+1)) ⇒ dx=((2(s^2 +s+1))/((2s+1)^2 ))ds ... ⇒ =ln∣((2x^2 +2x-1+(2x+1)(√(x^2 +x+1)))/(2x^2 +2x+1+(2x+1)(√(x^2 +x+1))))∣+C
$$=\int\:\underset{} {\underbrace{\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}}}\:+\int\underset{} {\underbrace{\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}}} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid\:\:\mathrm{and}\:\:\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{ln}\mid\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}-\mathrm{1}+\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}+\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mid \\ $$$$\mathrm{say}\:\rightarrow\:\boldsymbol{\mathrm{s}}=\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\Rightarrow\:\mathrm{dx}=\frac{\mathrm{2}\left(\mathrm{s}^{\mathrm{2}} +\mathrm{s}+\mathrm{1}\right)}{\left(\mathrm{2s}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{ds} \\ $$$$…\:\Rightarrow\:=\mathrm{ln}\mid\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}-\mathrm{1}+\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}+\left(\mathrm{2x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mid+\mathbb{C} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 20/Sep/21
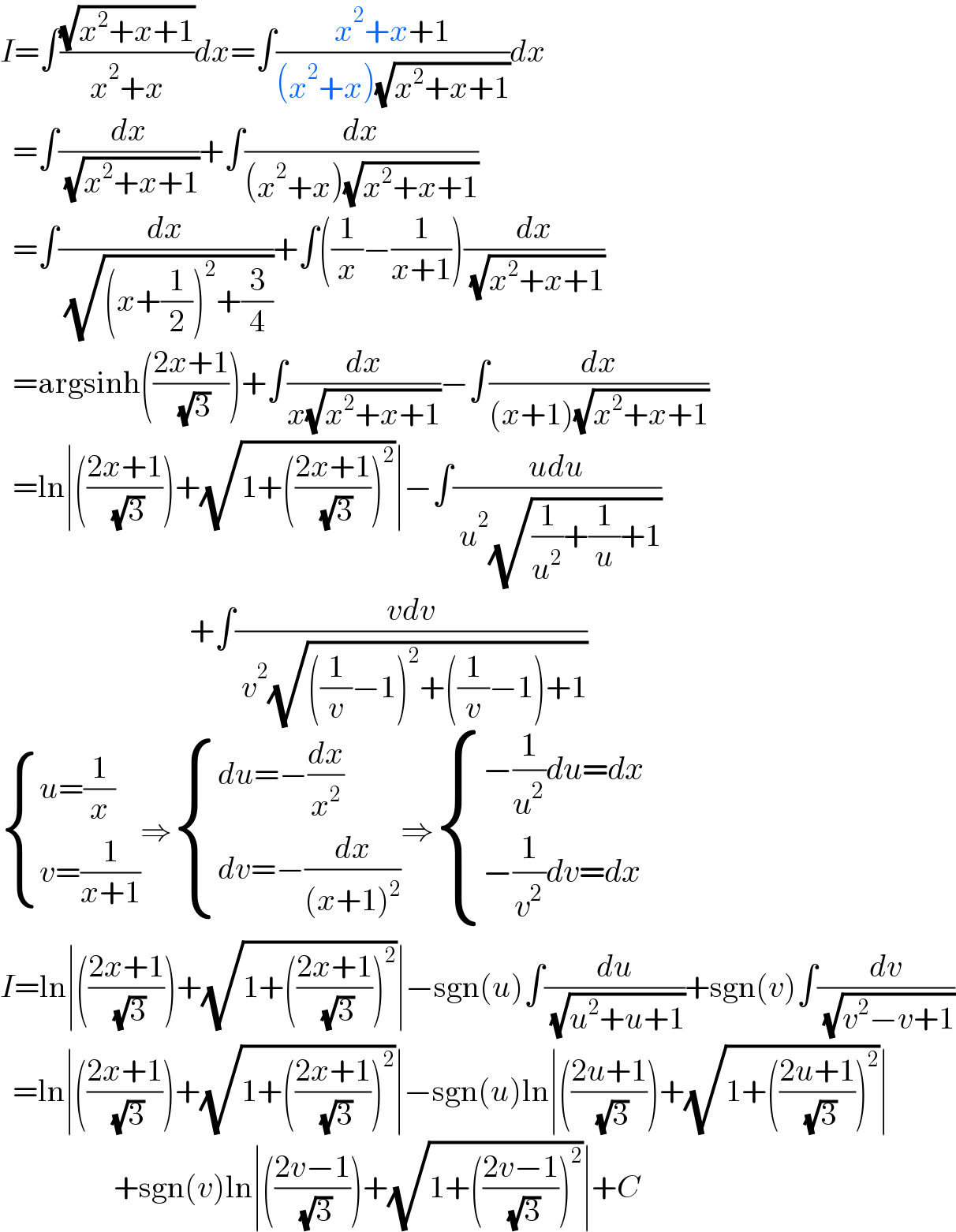
I=∫((√(x^2 +x+1))/(x^2 +x))dx=∫((x^2 +x+1)/((x^2 +x)(√(x^2 +x+1))))dx =∫(dx/( (√(x^2 +x+1))))+∫(dx/((x^2 +x)(√(x^2 +x+1)))) =∫(dx/( (√((x+(1/2))^2 +(3/4)))))+∫((1/x)−(1/(x+1)))(dx/( (√(x^2 +x+1)))) =argsinh(((2x+1)/( (√3))))+∫(dx/(x(√(x^2 +x+1))))−∫(dx/((x+1)(√(x^2 +x+1)))) =ln∣(((2x+1)/( (√3))))+(√(1+(((2x+1)/( (√3))))^2 ))∣−∫((udu)/( u^2 (√((1/u^2 )+(1/u)+1)))) +∫((vdv)/( v^2 (√(((1/v)−1)^2 +((1/v)−1)+1)))) { ((u=(1/x))),((v=(1/(x+1)))) :}⇒ { ((du=−(dx/x^2 ))),((dv=−(dx/((x+1)^2 )))) :}⇒ { ((−(1/u^2 )du=dx)),((−(1/v^2 )dv=dx)) :} I=ln∣(((2x+1)/( (√3))))+(√(1+(((2x+1)/( (√3))))^2 ))∣−sgn(u)∫(du/( (√(u^2 +u+1))))+sgn(v)∫(dv/( (√(v^2 −v+1)))) =ln∣(((2x+1)/( (√3))))+(√(1+(((2x+1)/( (√3))))^2 ))∣−sgn(u)ln∣(((2u+1)/( (√3))))+(√(1+(((2u+1)/( (√3))))^2 ))∣ +sgn(v)ln∣(((2v−1)/( (√3))))+(√(1+(((2v−1)/( (√3))))^2 ))∣+C
$${I}=\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{\mathrm{2}} +{x}}{dx}=\int\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$$$\:\:=\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$\:\:=\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}}+\int\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$\:\:=\mathrm{argsinh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}−\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$\:\:=\mathrm{ln}\mid\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\mid−\int\frac{{udu}}{\:{u}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}}{{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{{u}}+\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\int\frac{{vdv}}{\:{v}^{\mathrm{2}} \sqrt{\left(\frac{\mathrm{1}}{{v}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{v}}−\mathrm{1}\right)+\mathrm{1}}} \\ $$$$\begin{cases}{{u}=\frac{\mathrm{1}}{{x}}}\\{{v}=\frac{\mathrm{1}}{{x}+\mathrm{1}}}\end{cases}\Rightarrow\begin{cases}{{du}=−\frac{{dx}}{{x}^{\mathrm{2}} }}\\{{dv}=−\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}\end{cases}\Rightarrow\begin{cases}{−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }{du}={dx}}\\{−\frac{\mathrm{1}}{{v}^{\mathrm{2}} }{dv}={dx}}\end{cases} \\ $$$${I}=\mathrm{ln}\mid\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\mid−\mathrm{sgn}\left({u}\right)\int\frac{{du}}{\:\sqrt{{u}^{\mathrm{2}} +{u}+\mathrm{1}}}+\mathrm{sgn}\left({v}\right)\int\frac{{dv}}{\:\sqrt{{v}^{\mathrm{2}} −{v}+\mathrm{1}}} \\ $$$$\:\:=\mathrm{ln}\mid\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\mid−\mathrm{sgn}\left({u}\right)\mathrm{ln}\mid\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sgn}\left({v}\right)\mathrm{ln}\mid\left(\frac{\mathrm{2}{v}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{v}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\mid+{C} \\ $$
Answered by EDWIN88 last updated on 20/Sep/21
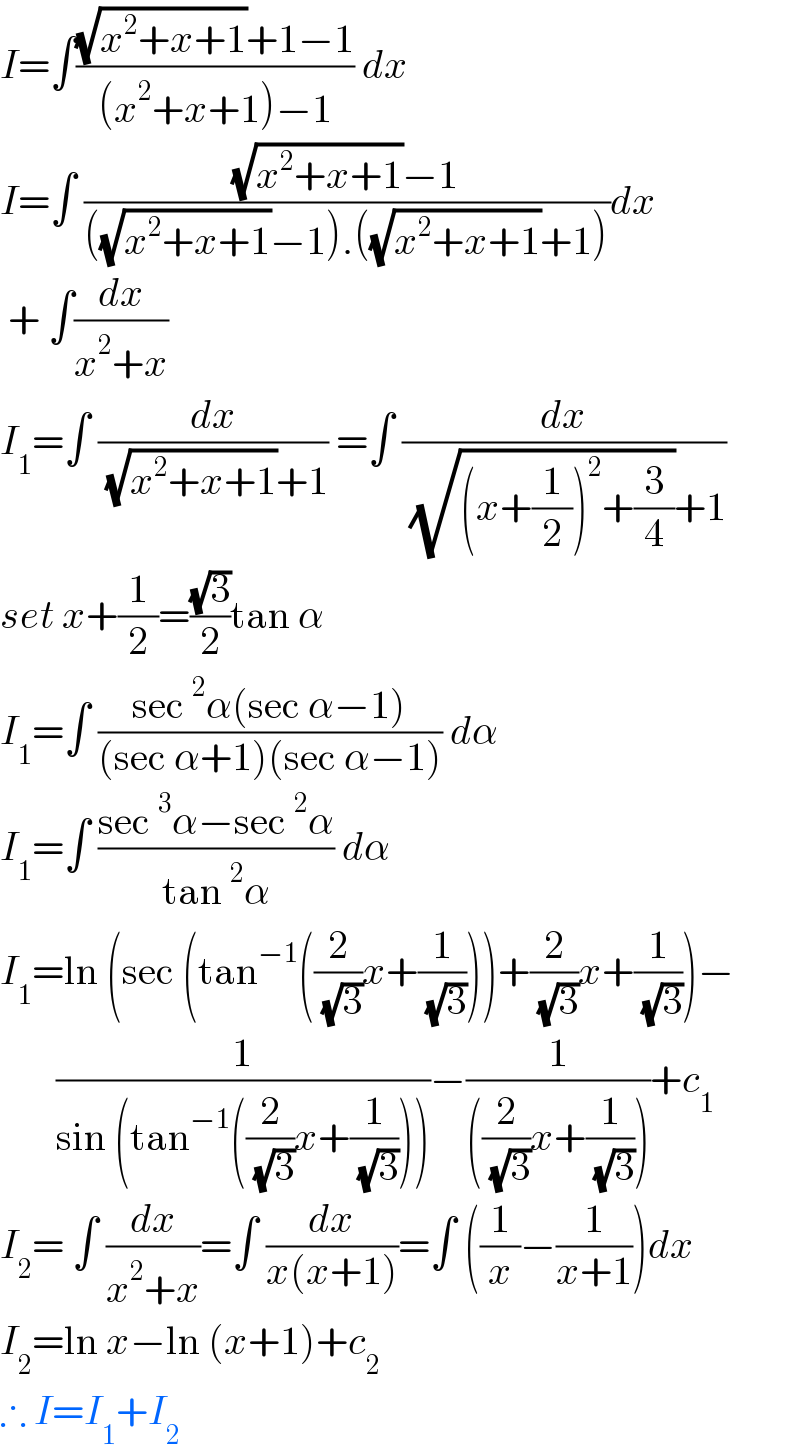
I=∫(((√(x^2 +x+1))+1−1)/((x^2 +x+1)−1)) dx I=∫ (((√(x^2 +x+1))−1)/(((√(x^2 +x+1))−1).((√(x^2 +x+1))+1)))dx + ∫(dx/(x^2 +x)) I_1 =∫ (dx/( (√(x^2 +x+1))+1)) =∫ (dx/( (√((x+(1/2))^2 +(3/4)))+1)) set x+(1/2)=((√3)/2)tan α I_1 =∫ ((sec^2 α(sec α−1))/((sec α+1)(sec α−1))) dα I_1 =∫ ((sec^3 α−sec^2 α)/(tan^2 α)) dα I_1 =ln (sec (tan^(−1) ((2/( (√3)))x+(1/( (√3)))))+(2/( (√3)))x+(1/( (√3))))− (1/(sin (tan^(−1) ((2/( (√3)))x+(1/( (√3)))))))−(1/(((2/( (√3)))x+(1/( (√3))))))+c_1 I_2 = ∫ (dx/(x^2 +x))=∫ (dx/(x(x+1)))=∫ ((1/x)−(1/(x+1)))dx I_2 =ln x−ln (x+1)+c_2 ∴ I=I_1 +I_2
$${I}=\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\mathrm{1}−\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\mathrm{1}}\:{dx} \\ $$$${I}=\int\:\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\mathrm{1}}{\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\mathrm{1}\right).\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\mathrm{1}\right)}{dx} \\ $$$$\:+\:\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}} \\ $$$${I}_{\mathrm{1}} =\int\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\mathrm{1}}\:=\int\:\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}+\mathrm{1}} \\ $$$${set}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}\:\alpha\: \\ $$$${I}_{\mathrm{1}} =\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \alpha\left(\mathrm{sec}\:\alpha−\mathrm{1}\right)}{\left(\mathrm{sec}\:\alpha+\mathrm{1}\right)\left(\mathrm{sec}\:\alpha−\mathrm{1}\right)}\:{d}\alpha \\ $$$${I}_{\mathrm{1}} =\int\:\frac{\mathrm{sec}\:^{\mathrm{3}} \alpha−\mathrm{sec}\:^{\mathrm{2}} \alpha}{\mathrm{tan}\:^{\mathrm{2}} \alpha}\:{d}\alpha \\ $$$${I}_{\mathrm{1}} =\mathrm{ln}\:\left(\mathrm{sec}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)− \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{sin}\:\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)}−\frac{\mathrm{1}}{\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} +{x}}=\int\:\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)}=\int\:\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$$${I}_{\mathrm{2}} =\mathrm{ln}\:{x}−\mathrm{ln}\:\left({x}+\mathrm{1}\right)+{c}_{\mathrm{2}} \\ $$$$\therefore\:{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *