Question Number 160744 by cortano last updated on 05/Dec/21
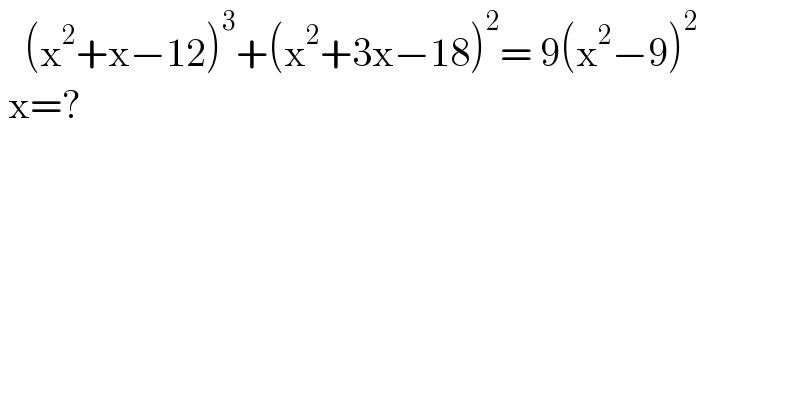
$$\:\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{12}\right)^{\mathrm{3}} +\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{18}\right)^{\mathrm{2}} =\:\mathrm{9}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{x}=?\: \\ $$
Commented by blackmamba last updated on 05/Dec/21
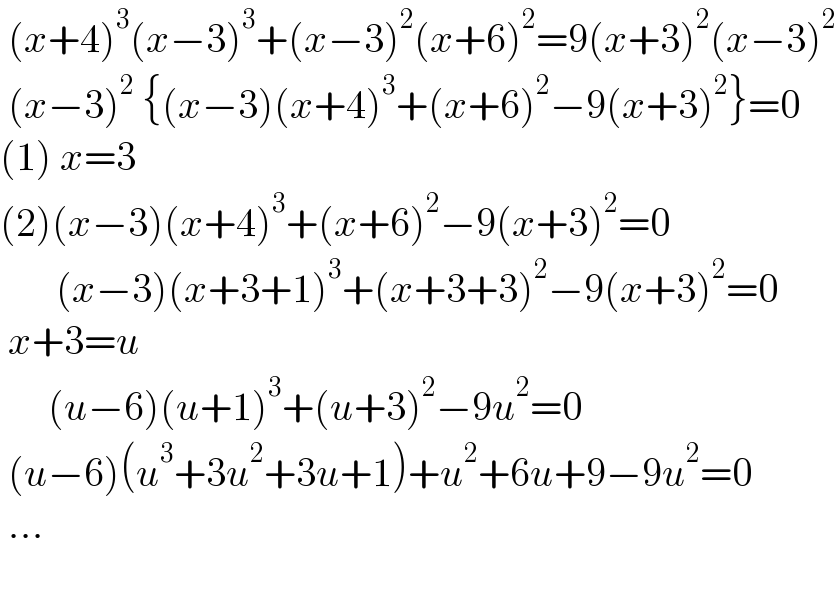
$$\:\left({x}+\mathrm{4}\right)^{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{2}} \left({x}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{9}\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\:\left({x}−\mathrm{3}\right)^{\mathrm{2}} \:\left\{\left({x}−\mathrm{3}\right)\left({x}+\mathrm{4}\right)^{\mathrm{3}} +\left({x}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{9}\left({x}+\mathrm{3}\right)^{\mathrm{2}} \right\}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{x}=\mathrm{3} \\ $$$$\left(\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}+\mathrm{4}\right)^{\mathrm{3}} +\left({x}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{9}\left({x}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}+\mathrm{1}\right)^{\mathrm{3}} +\left({x}+\mathrm{3}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}\left({x}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:{x}+\mathrm{3}={u}\: \\ $$$$\:\:\:\:\:\:\left({u}−\mathrm{6}\right)\left({u}+\mathrm{1}\right)^{\mathrm{3}} +\left({u}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{9}{u}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\left({u}−\mathrm{6}\right)\left({u}^{\mathrm{3}} +\mathrm{3}{u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{1}\right)+{u}^{\mathrm{2}} +\mathrm{6}{u}+\mathrm{9}−\mathrm{9}{u}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:…\: \\ $$$$\:\:\:\:\:\:\: \\ $$
Answered by MJS_new last updated on 06/Dec/21
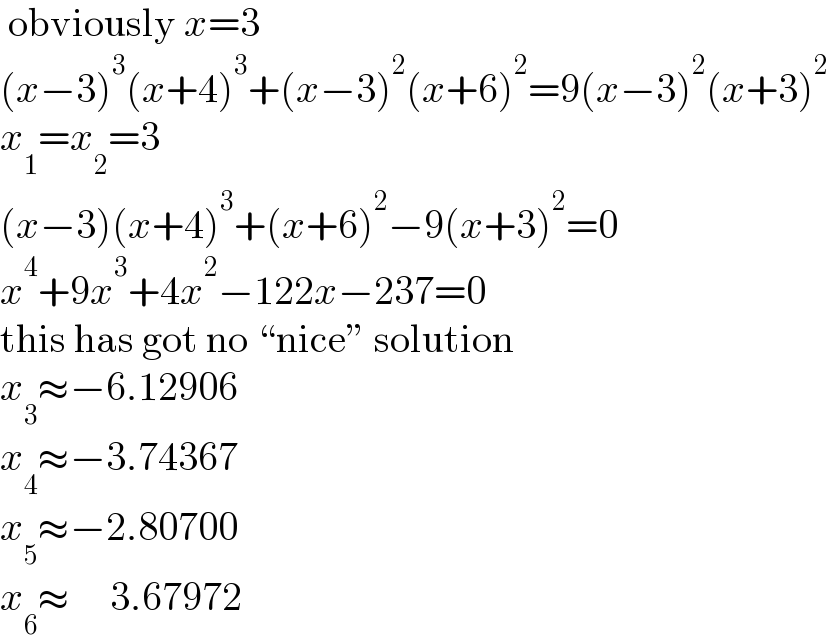
$$\:\mathrm{obviously}\:{x}=\mathrm{3} \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{3}} \left({x}+\mathrm{4}\right)^{\mathrm{3}} +\left({x}−\mathrm{3}\right)^{\mathrm{2}} \left({x}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{9}\left({x}−\mathrm{3}\right)^{\mathrm{2}} \left({x}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} ={x}_{\mathrm{2}} =\mathrm{3} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}+\mathrm{4}\right)^{\mathrm{3}} +\left({x}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{9}\left({x}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{9}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{122}{x}−\mathrm{237}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{got}\:\mathrm{no}\:“\mathrm{nice}''\:\mathrm{solution} \\ $$$${x}_{\mathrm{3}} \approx−\mathrm{6}.\mathrm{12906} \\ $$$${x}_{\mathrm{4}} \approx−\mathrm{3}.\mathrm{74367} \\ $$$${x}_{\mathrm{5}} \approx−\mathrm{2}.\mathrm{80700} \\ $$$${x}_{\mathrm{6}} \approx\:\:\:\:\:\mathrm{3}.\mathrm{67972} \\ $$
