Question Number 88307 by M±th+et£s last updated on 09/Apr/20
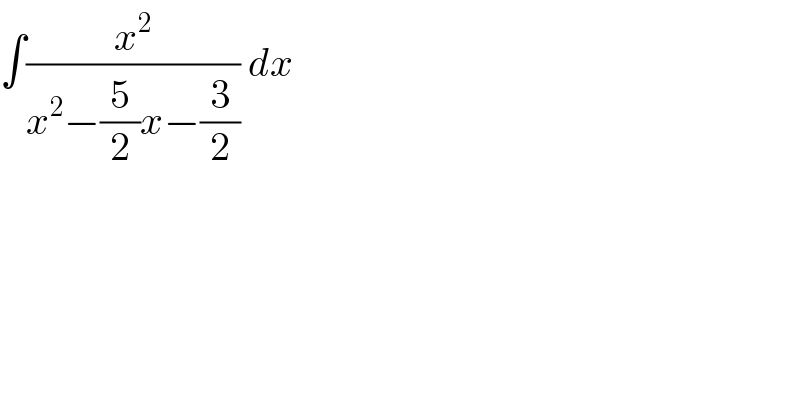
$$\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}{x}−\frac{\mathrm{3}}{\mathrm{2}}}\:{dx} \\ $$
Answered by TANMAY PANACEA. last updated on 09/Apr/20
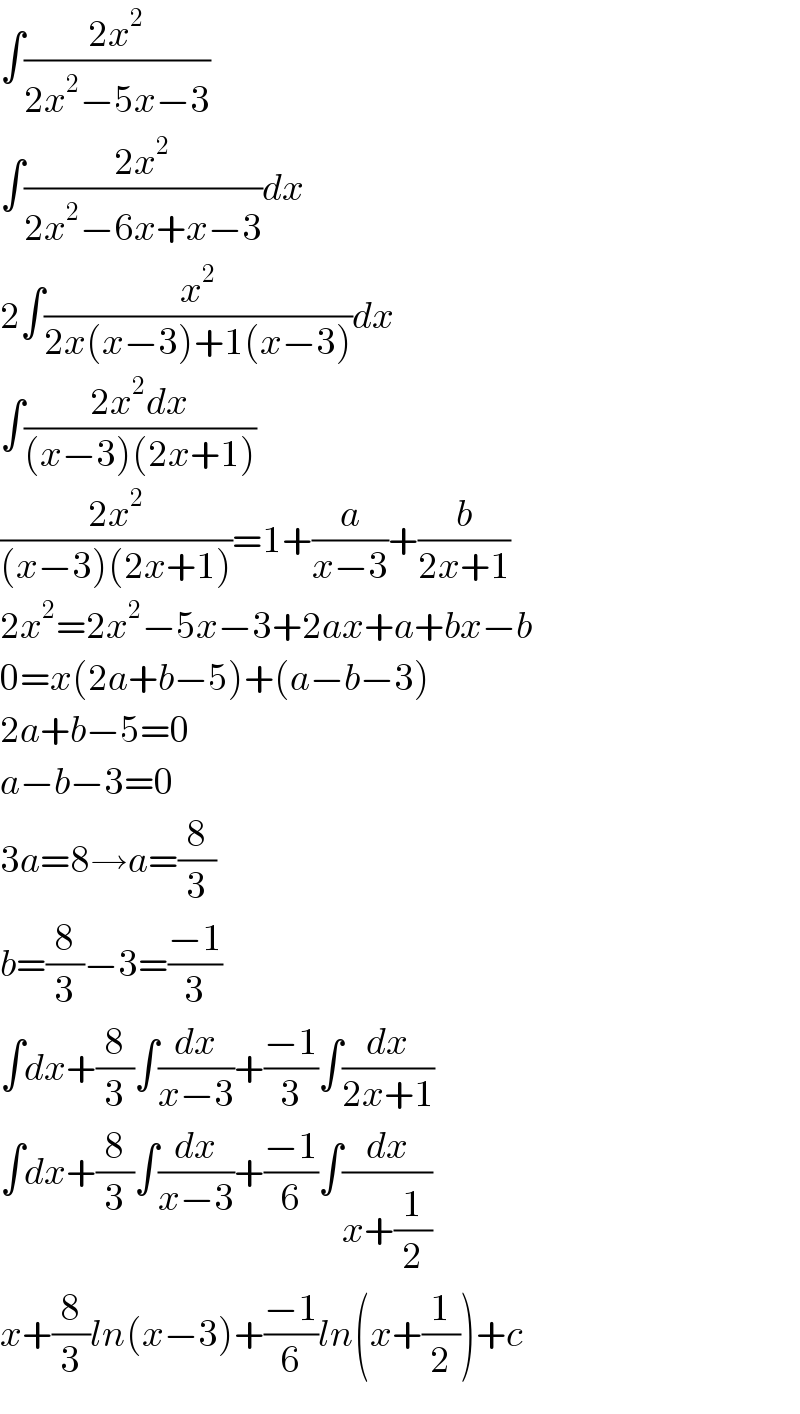
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}} \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+{x}−\mathrm{3}}{dx} \\ $$$$\mathrm{2}\int\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}\left({x}−\mathrm{3}\right)+\mathrm{1}\left({x}−\mathrm{3}\right)}{dx} \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} {dx}}{\left({x}−\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}−\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}=\mathrm{1}+\frac{{a}}{{x}−\mathrm{3}}+\frac{{b}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}+\mathrm{2}{ax}+{a}+{bx}−{b} \\ $$$$\mathrm{0}={x}\left(\mathrm{2}{a}+{b}−\mathrm{5}\right)+\left({a}−{b}−\mathrm{3}\right) \\ $$$$\mathrm{2}{a}+{b}−\mathrm{5}=\mathrm{0} \\ $$$${a}−{b}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{a}=\mathrm{8}\rightarrow{a}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$${b}=\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{3}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\int{dx}+\frac{\mathrm{8}}{\mathrm{3}}\int\frac{{dx}}{{x}−\mathrm{3}}+\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$$\int{dx}+\frac{\mathrm{8}}{\mathrm{3}}\int\frac{{dx}}{{x}−\mathrm{3}}+\frac{−\mathrm{1}}{\mathrm{6}}\int\frac{{dx}}{{x}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${x}+\frac{\mathrm{8}}{\mathrm{3}}{ln}\left({x}−\mathrm{3}\right)+\frac{−\mathrm{1}}{\mathrm{6}}{ln}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{c} \\ $$
Commented by M±th+et£s last updated on 09/Apr/20

$${god}\:{bless}\:{you} \\ $$
