Question Number 158176 by Odhiambojr last updated on 31/Oct/21
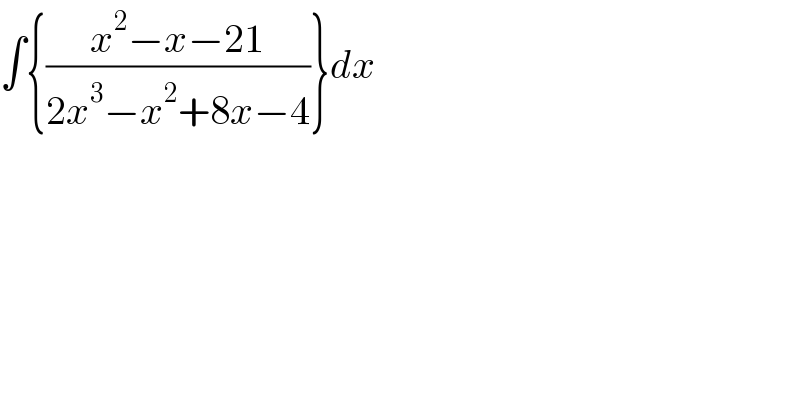
$$\int\left\{\frac{{x}^{\mathrm{2}} −{x}−\mathrm{21}}{\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{4}}\right\}{dx}\: \\ $$
Answered by MJS_new last updated on 31/Oct/21
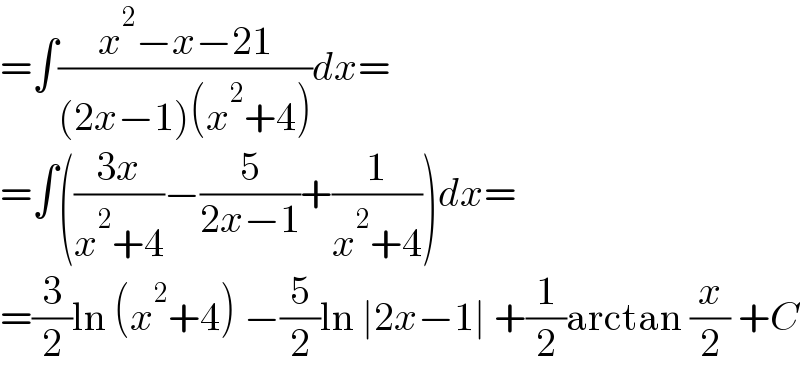
$$=\int\frac{{x}^{\mathrm{2}} −{x}−\mathrm{21}}{\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}= \\ $$$$=\int\left(\frac{\mathrm{3}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{5}}{\mathrm{2}{x}−\mathrm{1}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}\right){dx}= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{4}\right)\:−\frac{\mathrm{5}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{2}{x}−\mathrm{1}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{{x}}{\mathrm{2}}\:+{C} \\ $$
