Menu Close

x-2-x-2y-y-2-y-2z-z-2-z-2x-x-y-z-

Tinku Tara 0 Comments
Pin




Question Number 172312 by naka3546 last updated on 25/Jun/22
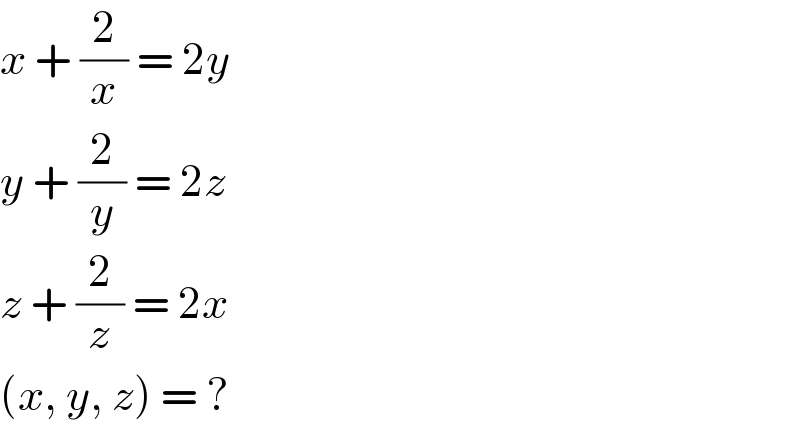
x + (2/x) = 2y y + (2/y) = 2z z + (2/z) = 2x (x, y, z) = ?
$${x}\:+\:\frac{\mathrm{2}}{{x}}\:=\:\mathrm{2}{y} \\ $$$${y}\:+\:\frac{\mathrm{2}}{{y}}\:=\:\mathrm{2}{z} \\ $$$${z}\:+\:\frac{\mathrm{2}}{{z}}\:=\:\mathrm{2}{x} \\ $$$$\left({x},\:{y},\:{z}\right)\:=\:? \\ $$
Commented by MJS_new last updated on 25/Jun/22
there are also solutions ∉R
$$\mathrm{there}\:\mathrm{are}\:\mathrm{also}\:\mathrm{solutions}\:\notin\mathbb{R} \\ $$
Commented by naka3546 last updated on 25/Jun/22
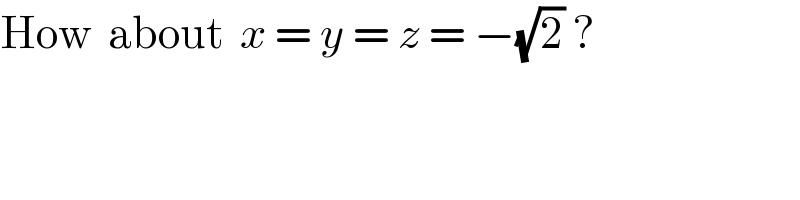
How about x = y = z = −(√2) ?
$$\mathrm{How}\:\:\mathrm{about}\:\:{x}\:=\:{y}\:=\:{z}\:=\:−\sqrt{\mathrm{2}}\:? \\ $$
Commented by infinityaction last updated on 25/Jun/22
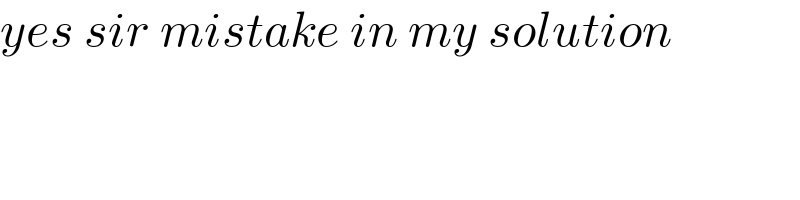
yes sir mistake in my solution
$${yes}\:{sir}\:{mistake}\:{in}\:{my}\:{solution} \\ $$
Commented by Tawa11 last updated on 25/Jun/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by infinityaction last updated on 25/Jun/22
share your solution sir
$${share}\:{your}\:{solution}\:{sir} \\ $$
Commented by MJS_new last updated on 25/Jun/22
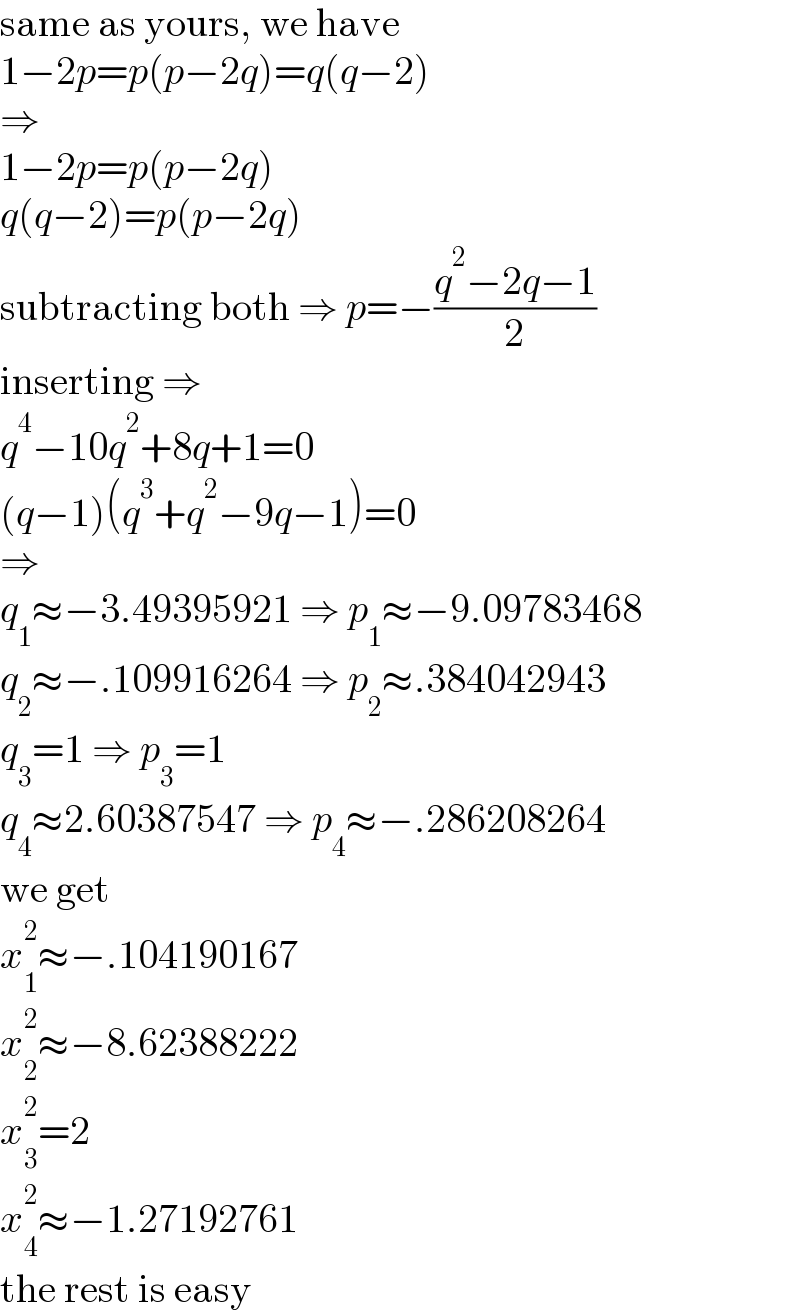
same as yours, we have 1−2p=p(p−2q)=q(q−2) ⇒ 1−2p=p(p−2q) q(q−2)=p(p−2q) subtracting both ⇒ p=−((q^2 −2q−1)/2) inserting ⇒ q^4 −10q^2 +8q+1=0 (q−1)(q^3 +q^2 −9q−1)=0 ⇒ q_1 ≈−3.49395921 ⇒ p_1 ≈−9.09783468 q_2 ≈−.109916264 ⇒ p_2 ≈.384042943 q_3 =1 ⇒ p_3 =1 q_4 ≈2.60387547 ⇒ p_4 ≈−.286208264 we get x_1 ^2 ≈−.104190167 x_2 ^2 ≈−8.62388222 x_3 ^2 =2 x_4 ^2 ≈−1.27192761 the rest is easy
$$\mathrm{same}\:\mathrm{as}\:\mathrm{yours},\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{1}−\mathrm{2}{p}={p}\left({p}−\mathrm{2}{q}\right)={q}\left({q}−\mathrm{2}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{1}−\mathrm{2}{p}={p}\left({p}−\mathrm{2}{q}\right) \\ $$$${q}\left({q}−\mathrm{2}\right)={p}\left({p}−\mathrm{2}{q}\right) \\ $$$$\mathrm{subtracting}\:\mathrm{both}\:\Rightarrow\:{p}=−\frac{{q}^{\mathrm{2}} −\mathrm{2}{q}−\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{inserting}\:\Rightarrow\: \\ $$$${q}^{\mathrm{4}} −\mathrm{10}{q}^{\mathrm{2}} +\mathrm{8}{q}+\mathrm{1}=\mathrm{0} \\ $$$$\left({q}−\mathrm{1}\right)\left({q}^{\mathrm{3}} +{q}^{\mathrm{2}} −\mathrm{9}{q}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${q}_{\mathrm{1}} \approx−\mathrm{3}.\mathrm{49395921}\:\Rightarrow\:{p}_{\mathrm{1}} \approx−\mathrm{9}.\mathrm{09783468} \\ $$$${q}_{\mathrm{2}} \approx−.\mathrm{109916264}\:\Rightarrow\:{p}_{\mathrm{2}} \approx.\mathrm{384042943} \\ $$$${q}_{\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{p}_{\mathrm{3}} =\mathrm{1} \\ $$$${q}_{\mathrm{4}} \approx\mathrm{2}.\mathrm{60387547}\:\Rightarrow\:{p}_{\mathrm{4}} \approx−.\mathrm{286208264} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} \approx−.\mathrm{104190167} \\ $$$${x}_{\mathrm{2}} ^{\mathrm{2}} \approx−\mathrm{8}.\mathrm{62388222} \\ $$$${x}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{2} \\ $$$${x}_{\mathrm{4}} ^{\mathrm{2}} \approx−\mathrm{1}.\mathrm{27192761} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by MJS_new last updated on 25/Jun/22
you did not find out at first because p^2 =p=1
$$\mathrm{you}\:\mathrm{did}\:\mathrm{not}\:\mathrm{find}\:\mathrm{out}\:\mathrm{at}\:\mathrm{first}\:\mathrm{because}\:{p}^{\mathrm{2}} ={p}=\mathrm{1} \\ $$
Commented by MJS_new last updated on 25/Jun/22
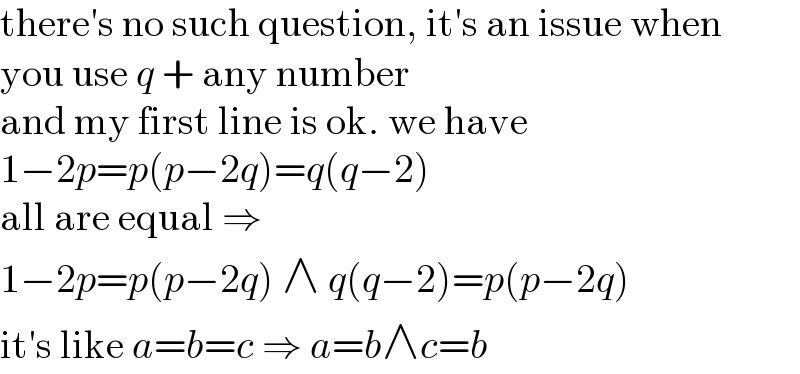
there′s no such question, it′s an issue when you use q + any number and my first line is ok. we have 1−2p=p(p−2q)=q(q−2) all are equal ⇒ 1−2p=p(p−2q) ∧ q(q−2)=p(p−2q) it′s like a=b=c ⇒ a=b∧c=b
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{such}\:\mathrm{question},\:\mathrm{it}'\mathrm{s}\:\mathrm{an}\:\mathrm{issue}\:\mathrm{when} \\ $$$$\mathrm{you}\:\mathrm{use}\:{q}\:+\:\mathrm{any}\:\mathrm{number} \\ $$$$\mathrm{and}\:\mathrm{my}\:\mathrm{first}\:\mathrm{line}\:\mathrm{is}\:\mathrm{ok}.\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{1}−\mathrm{2}{p}={p}\left({p}−\mathrm{2}{q}\right)={q}\left({q}−\mathrm{2}\right) \\ $$$$\mathrm{all}\:\mathrm{are}\:\mathrm{equal}\:\Rightarrow\: \\ $$$$\mathrm{1}−\mathrm{2}{p}={p}\left({p}−\mathrm{2}{q}\right)\:\wedge\:{q}\left({q}−\mathrm{2}\right)={p}\left({p}−\mathrm{2}{q}\right) \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{like}\:{a}={b}={c}\:\Rightarrow\:{a}={b}\wedge{c}={b} \\ $$
Commented by MJS_new last updated on 25/Jun/22
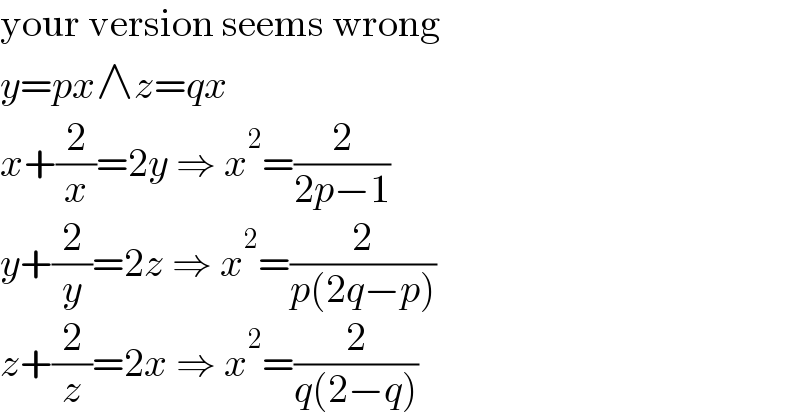
your version seems wrong y=px∧z=qx x+(2/x)=2y ⇒ x^2 =(2/(2p−1)) y+(2/y)=2z ⇒ x^2 =(2/(p(2q−p))) z+(2/z)=2x ⇒ x^2 =(2/(q(2−q)))
$$\mathrm{your}\:\mathrm{version}\:\mathrm{seems}\:\mathrm{wrong} \\ $$$${y}={px}\wedge{z}={qx} \\ $$$${x}+\frac{\mathrm{2}}{{x}}=\mathrm{2}{y}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{2}{p}−\mathrm{1}} \\ $$$${y}+\frac{\mathrm{2}}{{y}}=\mathrm{2}{z}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{2}}{{p}\left(\mathrm{2}{q}−{p}\right)} \\ $$$${z}+\frac{\mathrm{2}}{{z}}=\mathrm{2}{x}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{2}}{{q}\left(\mathrm{2}−{q}\right)} \\ $$
Commented by infinityaction last updated on 25/Jun/22
ok sir thanks
$${ok}\:{sir}\:{thanks} \\ $$
Commented by infinityaction last updated on 26/Jun/22
yes sir
$${yes}\:{sir}\: \\ $$
Answered by manxsol last updated on 29/Jan/23
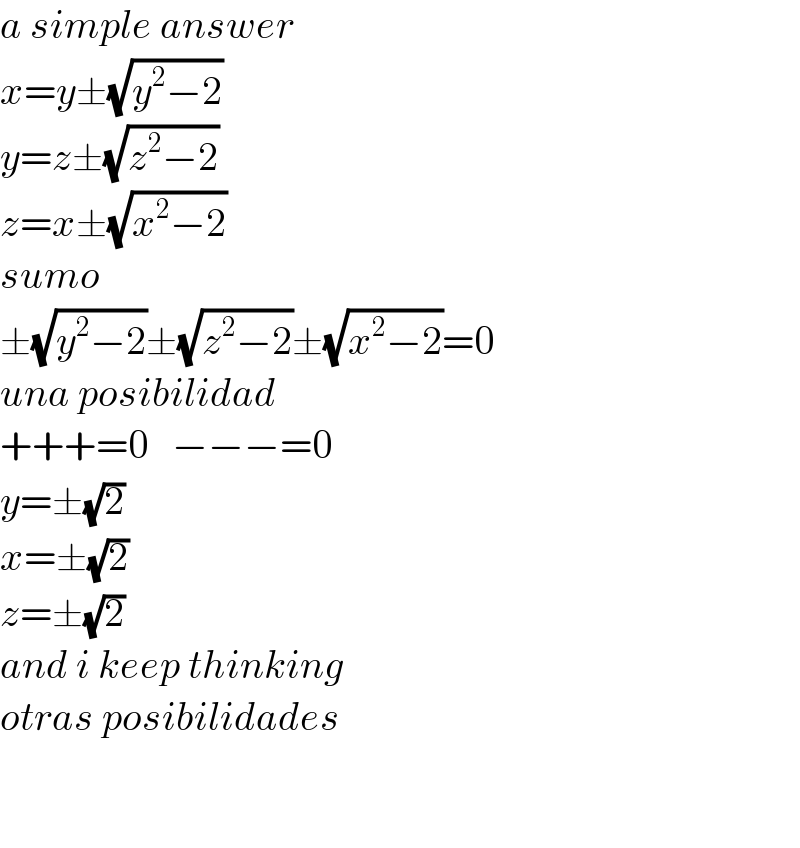
a simple answer x=y±(√(y^2 −2)) y=z±(√(z^2 −2)) z=x±(√(x^2 −2)) sumo ±(√(y^2 −2))±(√(z^2 −2))±(√(x^2 −2))=0 una posibilidad +++=0 −−−=0 y=±(√2) x=±(√2) z=±(√2) and i keep thinking otras posibilidades
$${a}\:{simple}\:{answer} \\ $$$${x}={y}\pm\sqrt{{y}^{\mathrm{2}} −\mathrm{2}} \\ $$$${y}={z}\pm\sqrt{{z}^{\mathrm{2}} −\mathrm{2}} \\ $$$${z}={x}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{2}} \\ $$$${sumo} \\ $$$$\pm\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\pm\sqrt{{z}^{\mathrm{2}} −\mathrm{2}}\pm\sqrt{{x}^{\mathrm{2}} −\mathrm{2}}=\mathrm{0} \\ $$$${una}\:{posibilidad} \\ $$$$+++=\mathrm{0}\:\:\:−−−=\mathrm{0} \\ $$$${y}=\pm\sqrt{\mathrm{2}} \\ $$$${x}=\pm\sqrt{\mathrm{2}} \\ $$$${z}=\pm\sqrt{\mathrm{2}} \\ $$$${and}\:{i}\:{keep}\:{thinking}\: \\ $$$${otras}\:{posibilidades} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *