x-2-x-4-dx-

Question Number 117053 by bemath last updated on 09/Oct/20

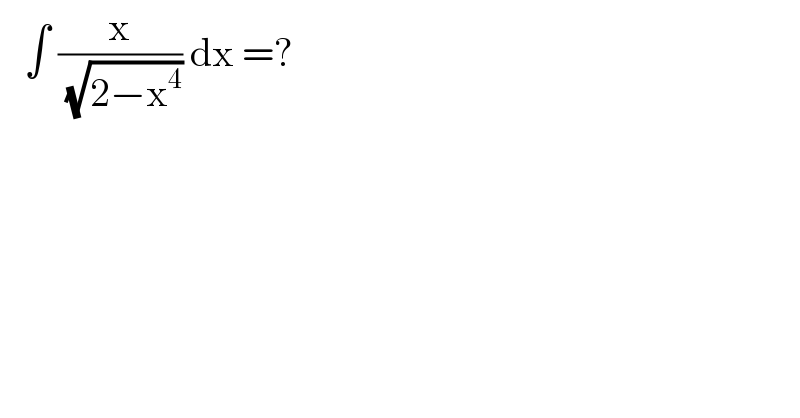
$$\:\:\:\int\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{4}} }}\:\mathrm{dx}\:=? \\ $$

Answered by Lordose last updated on 09/Oct/20

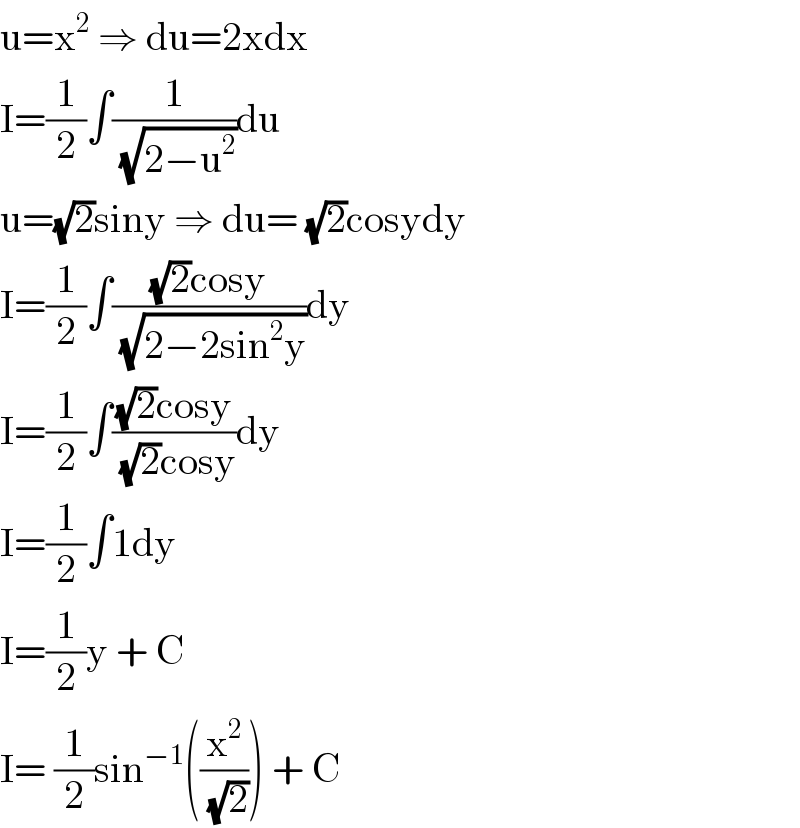
u=x^2 ⇒ du=2xdx I=(1/2)∫(1/( (√(2−u^2 ))))du u=(√2)siny ⇒ du= (√2)cosydy I=(1/2)∫(((√2)cosy)/( (√(2−2sin^2 y))))dy I=(1/2)∫(((√2)cosy)/( (√2)cosy))dy I=(1/2)∫1dy I=(1/2)y + C I= (1/2)sin^(−1) ((x^2 /( (√2)))) + C

$$\mathrm{u}=\mathrm{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{du}=\mathrm{2xdx} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−\mathrm{u}^{\mathrm{2}} }}\mathrm{du} \\ $$$$\mathrm{u}=\sqrt{\mathrm{2}}\mathrm{siny}\:\Rightarrow\:\mathrm{du}=\:\sqrt{\mathrm{2}}\mathrm{cosydy} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{2}}\mathrm{cosy}}{\:\sqrt{\mathrm{2}−\mathrm{2sin}^{\mathrm{2}} \mathrm{y}}}\mathrm{dy} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{2}}\mathrm{cosy}}{\:\sqrt{\mathrm{2}}\mathrm{cosy}}\mathrm{dy} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{1dy} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{y}\:+\:\mathrm{C} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}\right)\:+\:\mathrm{C} \\ $$

Answered by bobhans last updated on 09/Oct/20

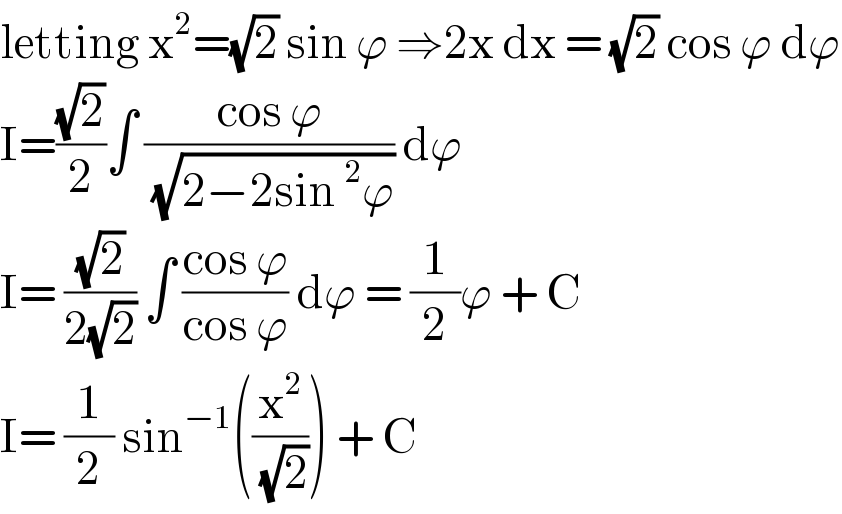
letting x^2 =(√2) sin ϕ ⇒2x dx = (√2) cos ϕ dϕ I=((√2)/2)∫ ((cos ϕ)/( (√(2−2sin^2 ϕ)))) dϕ I= ((√2)/(2(√2))) ∫ ((cos ϕ)/(cos ϕ)) dϕ = (1/2)ϕ + C I= (1/2) sin^(−1) ((x^2 /( (√2)))) + C

$$\mathrm{letting}\:\mathrm{x}^{\mathrm{2}} =\sqrt{\mathrm{2}}\:\mathrm{sin}\:\varphi\:\Rightarrow\mathrm{2x}\:\mathrm{dx}\:=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\varphi\:\mathrm{d}\varphi \\ $$$$\mathrm{I}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\:\frac{\mathrm{cos}\:\varphi}{\:\sqrt{\mathrm{2}−\mathrm{2sin}\:^{\mathrm{2}} \varphi}}\:\mathrm{d}\varphi\: \\ $$$$\mathrm{I}=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\frac{\mathrm{cos}\:\varphi}{\mathrm{cos}\:\varphi}\:\mathrm{d}\varphi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\varphi\:+\:\mathrm{C} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}\right)\:+\:\mathrm{C}\: \\ $$

Answered by 1549442205PVT last updated on 09/Oct/20

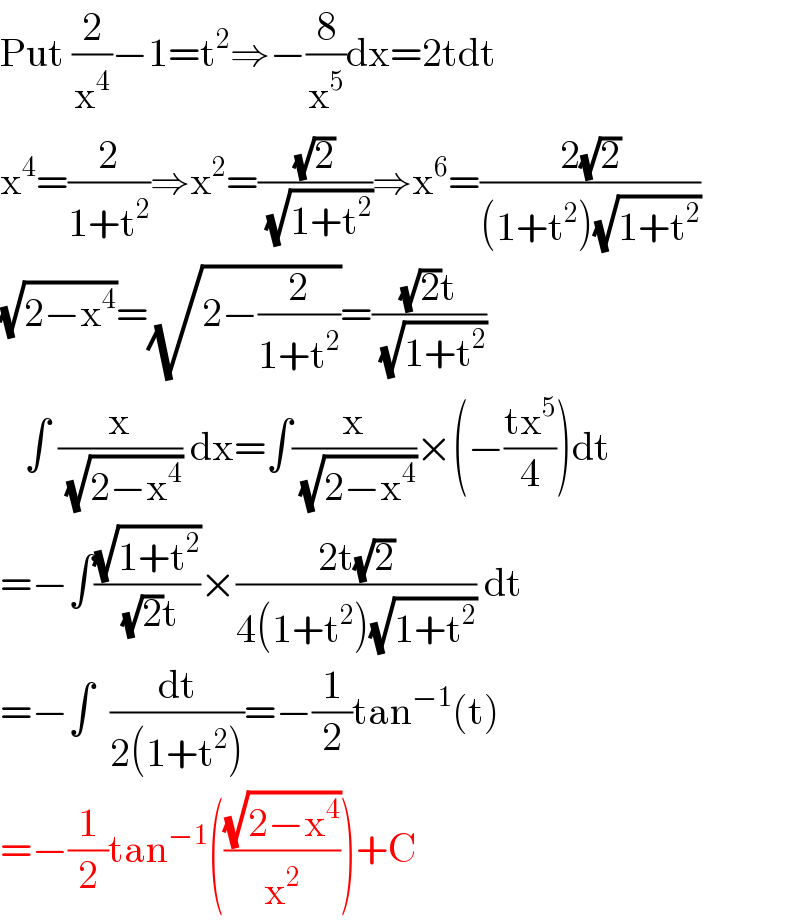
Put (2/x^4 )−1=t^2 ⇒−(8/x^5 )dx=2tdt x^4 =(2/(1+t^2 ))⇒x^2 =((√2)/( (√(1+t^2 ))))⇒x^6 =((2(√2))/((1+t^2 )(√(1+t^2 )))) (√(2−x^4 ))=(√(2−(2/(1+t^2 ))))=(((√2)t)/( (√(1+t^2 )))) ∫ (x/( (√(2−x^4 )))) dx=∫(x/( (√(2−x^4 ))))×(−((tx^5 )/4))dt =−∫((√(1+t^2 ))/( (√2)t))×((2t(√2))/(4(1+t^2 )(√(1+t^2 )))) dt =−∫ (dt/(2(1+t^2 )))=−(1/2)tan^(−1) (t) =−(1/2)tan^(−1) (((√(2−x^4 ))/x^2 ))+C

$$\mathrm{Put}\:\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{4}} }−\mathrm{1}=\mathrm{t}^{\mathrm{2}} \Rightarrow−\frac{\mathrm{8}}{\mathrm{x}^{\mathrm{5}} }\mathrm{dx}=\mathrm{2tdt} \\ $$$$\mathrm{x}^{\mathrm{4}} =\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\Rightarrow\mathrm{x}^{\mathrm{6}} =\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{4}} }=\sqrt{\mathrm{2}−\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{2}}\mathrm{t}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }} \\ $$$$\:\:\:\int\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{4}} }}\:\mathrm{dx}=\int\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{4}} }}×\left(−\frac{\mathrm{tx}^{\mathrm{5}} }{\mathrm{4}}\right)\mathrm{dt} \\ $$$$=−\int\frac{\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}\mathrm{t}}×\frac{\mathrm{2t}\sqrt{\mathrm{2}}}{\mathrm{4}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt} \\ $$$$=−\int\:\:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{t}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{C} \\ $$

Answered by Dwaipayan Shikari last updated on 09/Oct/20

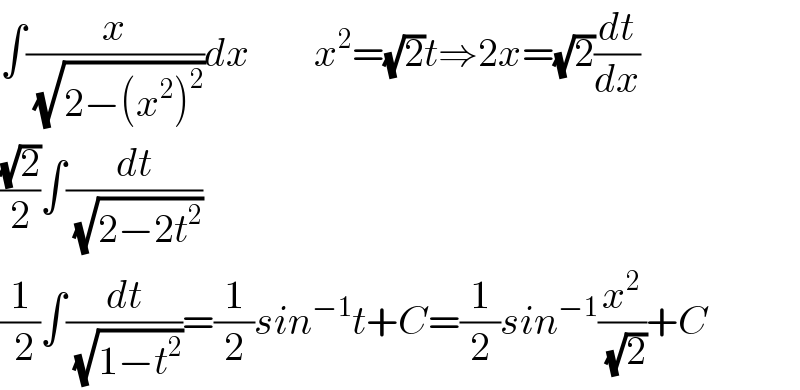
∫(x/( (√(2−(x^2 )^2 ))))dx x^2 =(√2)t⇒2x=(√2)(dt/dx) ((√2)/2)∫(dt/( (√(2−2t^2 )))) (1/( 2))∫(dt/( (√(1−t^2 ))))=(1/2)sin^(−1) t+C=(1/2)sin^(−1) (x^2 /( (√2)))+C

$$\int\frac{{x}}{\:\sqrt{\mathrm{2}−\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} }}{dx}\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\sqrt{\mathrm{2}}{t}\Rightarrow\mathrm{2}{x}=\sqrt{\mathrm{2}}\frac{{dt}}{{dx}} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{2}}\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} {t}+{C}=\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply