Menu Close

x-2-x-6-5-1-6-dx-

Tinku Tara 0 Comments
Pin




Question Number 180379 by cortano1 last updated on 11/Nov/22
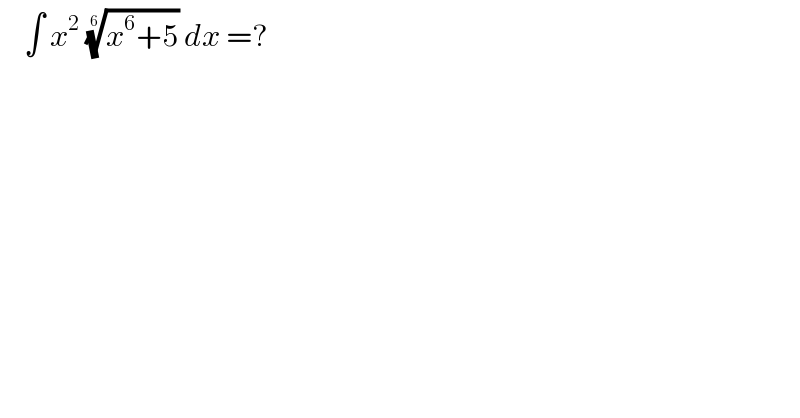
∫ x^2 ((x^6 +5))^(1/6) dx =?
$$\:\:\:\:\int\:{x}^{\mathrm{2}} \:\sqrt[{\mathrm{6}}]{{x}^{\mathrm{6}} +\mathrm{5}}\:{dx}\:=? \\ $$
Answered by Ar Brandon last updated on 11/Nov/22
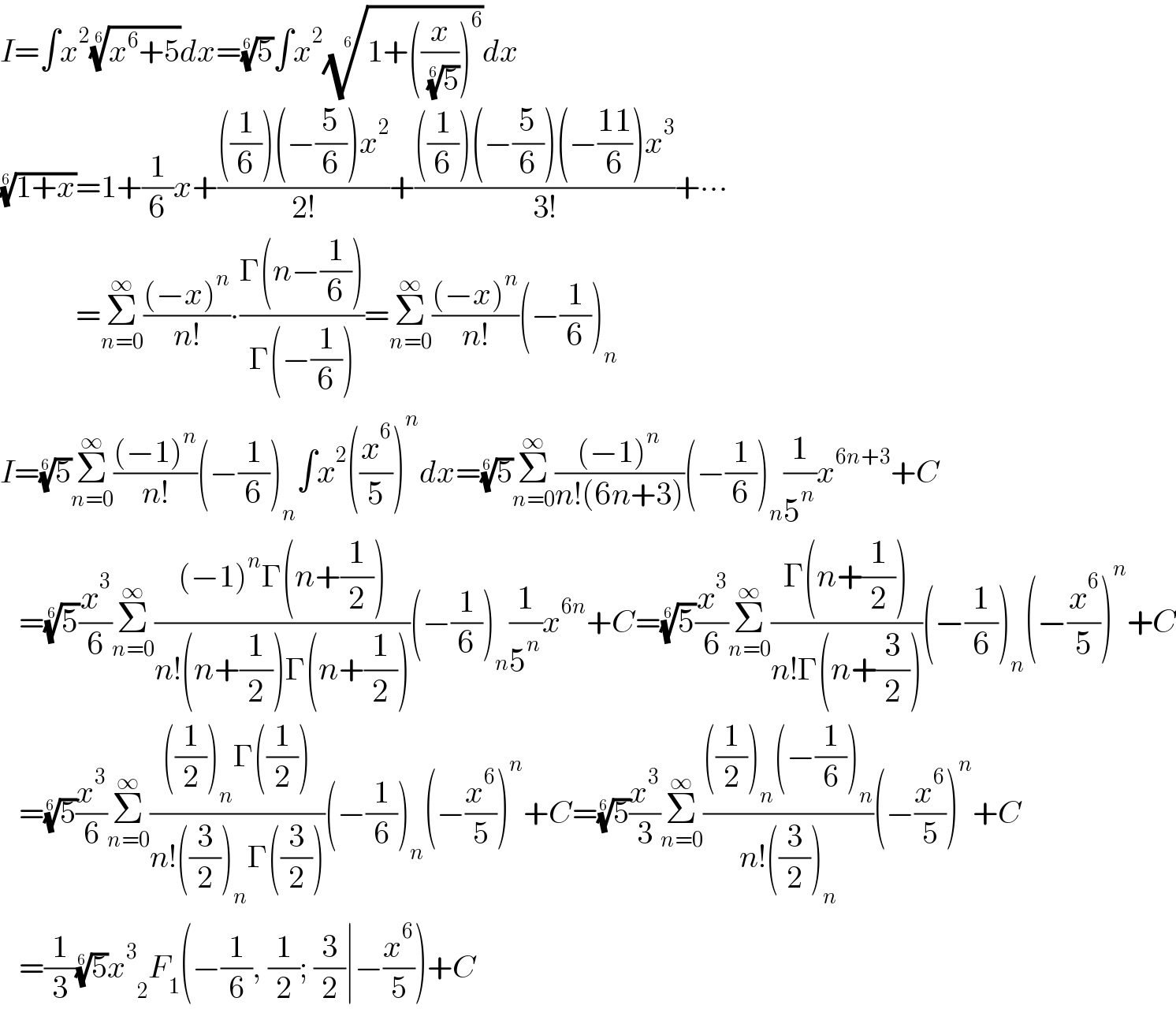
I=∫x^2 ((x^6 +5))^(1/6) dx=(5)^(1/6) ∫x^2 ((1+((x/( (5)^(1/6) )))^6 ))^(1/6) dx ((1+x))^(1/6) =1+(1/6)x+((((1/6))(−(5/6))x^2 )/(2!))+((((1/6))(−(5/6))(−((11)/6))x^3 )/(3!))+∙∙∙ =Σ_(n=0) ^∞ (((−x)^n )/(n!))∙((Γ(n−(1/6)))/(Γ(−(1/6))))=Σ_(n=0) ^∞ (((−x)^n )/(n!))(−(1/6))_n I=(5)^(1/6) Σ_(n=0) ^∞ (((−1)^n )/(n!))(−(1/6))_n ∫x^2 ((x^6 /5))^n dx=(5)^(1/6) Σ_(n=0) ^∞ (((−1)^n )/(n!(6n+3)))(−(1/6))_n (1/5^n )x^(6n+3) +C =(5)^(1/6) (x^3 /6)Σ_(n=0) ^∞ (((−1)^n Γ(n+(1/2)))/(n!(n+(1/2))Γ(n+(1/2))))(−(1/6))_n (1/5^n )x^(6n) +C=(5)^(1/6) (x^3 /6)Σ_(n=0) ^∞ ((Γ(n+(1/2)))/(n!Γ(n+(3/2))))(−(1/6))_n (−(x^6 /5))^n +C =(5)^(1/6) (x^3 /6)Σ_(n=0) ^∞ ((((1/2))_n Γ((1/2)))/(n!((3/2))_n Γ((3/2))))(−(1/6))_n (−(x^6 /5))^n +C=(5)^(1/6) (x^3 /3)Σ_(n=0) ^∞ ((((1/2))_n (−(1/6))_n )/(n!((3/2))_n ))(−(x^6 /5))^n +C =(1/3)(5)^(1/6) x^3 _2 F_1 (−(1/6), (1/2); (3/2)∣−(x^6 /5))+C
$${I}=\int{x}^{\mathrm{2}} \sqrt[{\mathrm{6}}]{{x}^{\mathrm{6}} +\mathrm{5}}{dx}=\sqrt[{\mathrm{6}}]{\mathrm{5}}\int{x}^{\mathrm{2}} \sqrt[{\mathrm{6}}]{\mathrm{1}+\left(\frac{{x}}{\:\sqrt[{\mathrm{6}}]{\mathrm{5}}}\right)^{\mathrm{6}} }{dx} \\ $$$$\sqrt[{\mathrm{6}}]{\mathrm{1}+{x}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}{x}+\frac{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\left(−\frac{\mathrm{5}}{\mathrm{6}}\right){x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\left(−\frac{\mathrm{5}}{\mathrm{6}}\right)\left(−\frac{\mathrm{11}}{\mathrm{6}}\right){x}^{\mathrm{3}} }{\mathrm{3}!}+\centerdot\centerdot\centerdot \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{x}\right)^{{n}} }{{n}!}\centerdot\frac{\Gamma\left({n}−\frac{\mathrm{1}}{\mathrm{6}}\right)}{\Gamma\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{x}\right)^{{n}} }{{n}!}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \\ $$$${I}=\sqrt[{\mathrm{6}}]{\mathrm{5}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \int{x}^{\mathrm{2}} \left(\frac{{x}^{\mathrm{6}} }{\mathrm{5}}\right)^{{n}} {dx}=\sqrt[{\mathrm{6}}]{\mathrm{5}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left(\mathrm{6}{n}+\mathrm{3}\right)}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \frac{\mathrm{1}}{\mathrm{5}^{{n}} }{x}^{\mathrm{6}{n}+\mathrm{3}} +{C} \\ $$$$\:\:\:=\sqrt[{\mathrm{6}}]{\mathrm{5}}\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \frac{\mathrm{1}}{\mathrm{5}^{{n}} }{x}^{\mathrm{6}{n}} +{C}=\sqrt[{\mathrm{6}}]{\mathrm{5}}\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \left(−\frac{{x}^{\mathrm{6}} }{\mathrm{5}}\right)^{{n}} +{C} \\ $$$$\:\:\:=\sqrt[{\mathrm{6}}]{\mathrm{5}}\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} \Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}\left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} \left(−\frac{{x}^{\mathrm{6}} }{\mathrm{5}}\right)^{{n}} +{C}=\sqrt[{\mathrm{6}}]{\mathrm{5}}\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \left(−\frac{\mathrm{1}}{\mathrm{6}}\right)_{{n}} }{{n}!\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} }\left(−\frac{{x}^{\mathrm{6}} }{\mathrm{5}}\right)^{{n}} +{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\sqrt[{\mathrm{6}}]{\mathrm{5}}{x}^{\mathrm{3}} \underset{\mathrm{2}} {\:}{F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{6}},\:\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\mathrm{3}}{\mathrm{2}}\mid−\frac{{x}^{\mathrm{6}} }{\mathrm{5}}\right)+{C} \\ $$
Commented by cortano1 last updated on 12/Nov/22
waw
$$\mathrm{waw} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *