Question Number 97847 by bemath last updated on 10/Jun/20
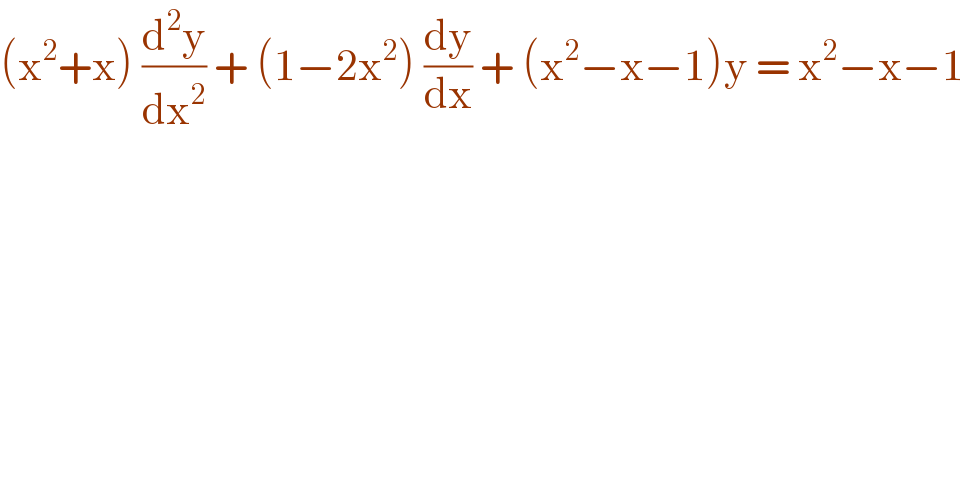
$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\:\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)\mathrm{y}\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1} \\ $$
Answered by niroj last updated on 10/Jun/20
![(x^2 +x)(d^2 y/dx^2 ) + (1−2x^2 ) (dy/dx) +(x^2 −x−1)y= x^2 −x−1 (d^2 y/dx^2 ) + (((1−2x^2 ))/(x^2 +x)) (dy/dx) + ((x^2 −x−1)/(x^2 +x)) y = ((x^2 −x−1)/(x^2 +x)) We know variable coefficient for CF If : 1+P+Q=0 then part of CF ,u=e^x let P= ((1−2x^2 )/(x^2 +x)) , Q= ((x^2 −x−1)/(x^2 +x)) and R= ((x^2 −x−1)/(x^2 +x)) 1+((1−2x^2 )/(x^2 +x))+((x^2 −x−1)/(x^2 +x))= ((x^2 +x+1−2x^2 +x^2 −x−1)/(x^2 +x))= (0/(x^2 +x))=0. ∵1+P+Q=0 is satisfy complete function y= uv y= e^x v.......(i) we know special case : (d^2 v/dx^2 )+(p+(2/u).(du/dx))(dv/dx)= (R/u) (d^2 v/dx^2 )+(((1−2x^2 )/(x^2 +x)) + (2/e^x ) .e^x )(dv/dx)= ((x^2 −x−1)/(e^x (x^2 +x))) (d^2 v/dx^2 ) +(((2x^2 +2x+1−2x^2 )/(x^2 +x)))(dv/dx) = ((x^2 −x−1)/(e^x (x^2 +x))) (d^2 v/dx^2 ) + ((2x+1)/(x^2 +x)) (dv/dx) = ((x^2 −x−1)/(e^x (x^2 +x))) Now we reduces linear form, Put , (dv/dx)= t ⇒ (d^2 v/dx^2 )= (dt/dx) (dt/dx) + ((2x+1)/(x^2 +x )). t = ((x^2 −x−1)/(e^x (x^2 +x))) IF= e^(∫Pdx) = e^(∫((2x+1)/(x^2 +x))dx) =e^(log (x^2 +x)) IF= x^2 +x t.IF= ∫IF.Qdx+C_1 t.(x^2 +x)= ∫(x^2 +x).((x^2 −x−1)/(e^x (x^2 +x)))dx+C_1 t(x^2 +x)= ∫ ((x^2 −x−1)/e^x )dx+C_1 t(x^2 +x)= ∫ x^2 e^(−x) dx−∫xe^(−x) dx−∫e^(−x) dx+C_1 t(x^2 +x)= [x^2 .(−e^(−x) )−∫2x.(−e^(−x) )dx]−∫xe^(−x) dx−(−e^(−x) )+C_1 t(x^2 +x)= −x^2 e^(−x) +2∫xe^(−x) dx−∫xe^(−x) dx+e^(−x) +C_1 t(x^2 +x)= −x^2 e^(−x) +∫xe^(−x) dx+e^(−x) +C_1 t(x^2 +x)= −x^2 e^(−x) +x(−e^x )−∫1.(−e^(−x) )dx+e^(−x) +C_1 t(x^2 +x)= −x^2 e^(−x) −xe^(−x) −e^(−x) +e^(−x) +C_1 t(x^2 +x)= −x^2 e^(−x) −xe^(−x) +C_1 t= ((−xe^(−x) (x+1))/(x(x+1)))+C_1 (1/(x(x+1))) (dv/dx) = −e^(−x) +C_1 (1/(x(x+1))) ∫dv = −∫e^(−x) dx+C_1 ∫ (1/(x(x+1)))dx+C_2 v= −(−e^(−x) )+C_1 [ ∫(1/x)dx−∫(1/(x+1))dx]+C_2 v= e^(−x) +C_1 { log x−log(x+1)}+C_2 v= e^(−x) +C_1 log (x/(x+1))+C_2 Now, again put value of v in eq^n (i) y=e^x v.....(i) y= e^x (e^(−x) +C_1 log (x/(x+1))+C_2 ) y = 1+ C_1 e^x log (x/(x+1)) +C_(2 ) e^x //.](https://www.tinkutara.com/question/Q97946.png)
$$\:\:\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\:\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\right)\mathrm{y}=\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1} \\ $$$$\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\:\frac{\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:\mathrm{y}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}} \\ $$$$\:\:\:\mathrm{We}\:\mathrm{know}\:\mathrm{variable}\:\mathrm{coefficient}\:\mathrm{for}\:\mathrm{CF}\: \\ $$$$\:\mathrm{If}\::\:\mathrm{1}+\mathrm{P}+\mathrm{Q}=\mathrm{0}\:\:\mathrm{then}\:\mathrm{part}\:\mathrm{of}\:\mathrm{CF}\:,\mathrm{u}=\mathrm{e}^{\mathrm{x}} \\ $$$$\:\:\mathrm{let}\:\mathrm{P}=\:\:\frac{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:,\:\mathrm{Q}=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:\mathrm{and}\:\mathrm{R}=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}} \\ $$$$\:\:\mathrm{1}+\frac{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}=\:\frac{\mathrm{0}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}=\mathrm{0}. \\ $$$$\:\because\mathrm{1}+\mathrm{P}+\mathrm{Q}=\mathrm{0}\:\mathrm{is}\:\mathrm{satisfy}\: \\ $$$$\:\mathrm{complete}\:\mathrm{function}\: \\ $$$$\:\:\mathrm{y}=\:\mathrm{uv} \\ $$$$\:\:\mathrm{y}=\:\mathrm{e}^{\mathrm{x}} \mathrm{v}…….\left(\mathrm{i}\right) \\ $$$$\:\mathrm{we}\:\mathrm{know}\:\mathrm{special}\:\mathrm{case}\:: \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }+\left(\mathrm{p}+\frac{\mathrm{2}}{\mathrm{u}}.\frac{\mathrm{du}}{\mathrm{dx}}\right)\frac{\mathrm{dv}}{\mathrm{dx}}=\:\frac{\mathrm{R}}{\mathrm{u}} \\ $$$$\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }+\left(\frac{\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:+\:\frac{\mathrm{2}}{\mathrm{e}^{\mathrm{x}} }\:.\mathrm{e}^{\mathrm{x}} \right)\frac{\mathrm{dv}}{\mathrm{dx}}=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }\:+\left(\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\right)\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }\:+\:\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\mathrm{Now}\:\mathrm{we}\:\mathrm{reduces}\:\mathrm{linear}\:\mathrm{form}, \\ $$$$\:\:\:\:\mathrm{Put}\:,\:\frac{\mathrm{dv}}{\mathrm{dx}}=\:\mathrm{t}\:\Rightarrow\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{v}}{\mathrm{dx}^{\mathrm{2}} }=\:\frac{\mathrm{dt}}{\mathrm{dx}} \\ $$$$\:\:\frac{\mathrm{dt}}{\mathrm{dx}}\:+\:\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:}.\:\mathrm{t}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\:\mathrm{IF}=\:\mathrm{e}^{\int\mathrm{Pdx}} =\:\mathrm{e}^{\int\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\mathrm{dx}} =\mathrm{e}^{\mathrm{log}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\:\mathrm{IF}=\:\mathrm{x}^{\mathrm{2}} +\mathrm{x} \\ $$$$\:\:\:\:\:\mathrm{t}.\mathrm{IF}=\:\int\mathrm{IF}.\mathrm{Qdx}+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\:\mathrm{t}.\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:\int\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right).\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)}\mathrm{dx}+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:\int\:\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}}{\mathrm{e}^{\mathrm{x}} }\mathrm{dx}+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:\int\:\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx}−\int\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}−\int\mathrm{e}^{−\mathrm{x}} \mathrm{dx}+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:\left[\mathrm{x}^{\mathrm{2}} .\left(−\mathrm{e}^{−\mathrm{x}} \right)−\int\mathrm{2x}.\left(−\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx}\right]−\int\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}−\left(−\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} +\mathrm{2}\int\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}−\int\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}+\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} +\int\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}+\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \\ $$$$\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} +\mathrm{x}\left(−\mathrm{e}^{\mathrm{x}} \right)−\int\mathrm{1}.\left(−\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx}+\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \\ $$$$\:\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \\ $$$$\:\:\mathrm{t}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)=\:−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \\ $$$$\:\:\mathrm{t}=\:\frac{−\mathrm{xe}^{−\mathrm{x}} \left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)}+\mathrm{C}_{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:−\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$\:\:\int\mathrm{dv}\:=\:−\int\mathrm{e}^{−\mathrm{x}} \mathrm{dx}+\mathrm{C}_{\mathrm{1}} \int\:\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx}+{C}_{\mathrm{2}} \\ $$$$\:\mathrm{v}=\:−\left(−\mathrm{e}^{−\mathrm{x}} \right)+\mathrm{C}_{\mathrm{1}} \left[\:\int\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}−\int\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\right]+{C}_{\mathrm{2}} \\ $$$$\:\mathrm{v}=\:\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \left\{\:\mathrm{log}\:\mathrm{x}−\mathrm{log}\left(\mathrm{x}+\mathrm{1}\right)\right\}+\mathrm{C}_{\mathrm{2}} \\ $$$$\:\mathrm{v}=\:\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \mathrm{log}\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}+\mathrm{C}_{\mathrm{2}} \\ $$$$\:\mathrm{Now},\:\mathrm{again}\:\mathrm{put}\:\mathrm{value}\:\mathrm{of}\:\mathrm{v}\:\mathrm{in}\:\mathrm{eq}^{\mathrm{n}} \left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{y}=\mathrm{e}^{\mathrm{x}} \mathrm{v}…..\left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{y}=\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{e}^{−\mathrm{x}} +\mathrm{C}_{\mathrm{1}} \mathrm{log}\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}+\mathrm{C}_{\mathrm{2}} \right) \\ $$$$\:\:\mathrm{y}\:=\:\mathrm{1}+\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:\mathrm{log}\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}\:+\mathrm{C}_{\mathrm{2}\:} \mathrm{e}^{\mathrm{x}} \:\://. \\ $$$$\: \\ $$$$ \\ $$$$ \\ $$$$\:\: \\ $$$$ \\ $$
Commented by niroj last updated on 11/Jun/20
thanks dear������
Commented by bemath last updated on 11/Jun/20

$$\mathrm{waw}===\mathrm{beautifull}\:\mathrm{solution} \\ $$
Commented by bemath last updated on 11/Jun/20

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
