Question Number 100660 by bobhans last updated on 28/Jun/20
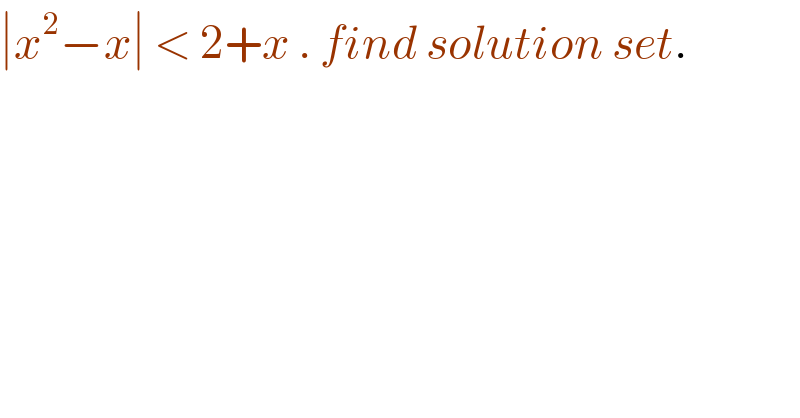
$$\mid{x}^{\mathrm{2}} −{x}\mid\:<\:\mathrm{2}+{x}\:.\:{find}\:{solution}\:{set}. \\ $$
Commented by bramlex last updated on 28/Jun/20
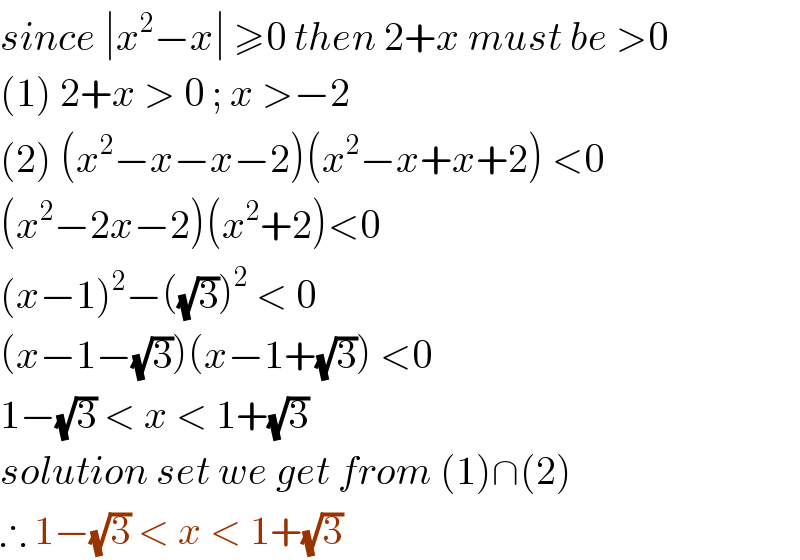
$${since}\:\mid{x}^{\mathrm{2}} −{x}\mid\:\geqslant\mathrm{0}\:{then}\:\mathrm{2}+{x}\:{must}\:{be}\:>\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}+{x}\:>\:\mathrm{0}\:;\:{x}\:>−\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\:\left({x}^{\mathrm{2}} −{x}−{x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} −{x}+{x}+\mathrm{2}\right)\:<\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)<\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:<\:\mathrm{0} \\ $$$$\left({x}−\mathrm{1}−\sqrt{\mathrm{3}}\right)\left({x}−\mathrm{1}+\sqrt{\mathrm{3}}\right)\:<\mathrm{0} \\ $$$$\mathrm{1}−\sqrt{\mathrm{3}}\:<\:{x}\:<\:\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$${solution}\:{set}\:{we}\:{get}\:{from}\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right) \\ $$$$\therefore\:\mathrm{1}−\sqrt{\mathrm{3}}\:<\:{x}\:<\:\mathrm{1}+\sqrt{\mathrm{3}}\: \\ $$
