Question Number 149040 by mathdanisur last updated on 02/Aug/21
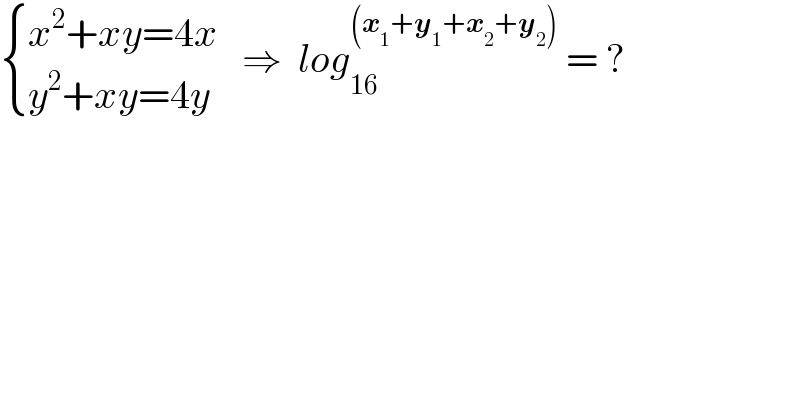
$$\begin{cases}{{x}^{\mathrm{2}} +{xy}=\mathrm{4}{x}}\\{{y}^{\mathrm{2}} +{xy}=\mathrm{4}{y}}\end{cases}\:\:\:\Rightarrow\:\:{log}_{\mathrm{16}} ^{\left(\boldsymbol{{x}}_{\mathrm{1}} +\boldsymbol{{y}}_{\mathrm{1}} +\boldsymbol{{x}}_{\mathrm{2}} +\boldsymbol{{y}}_{\mathrm{2}} \right)} \:=\:? \\ $$
Answered by bramlexs22 last updated on 02/Aug/21
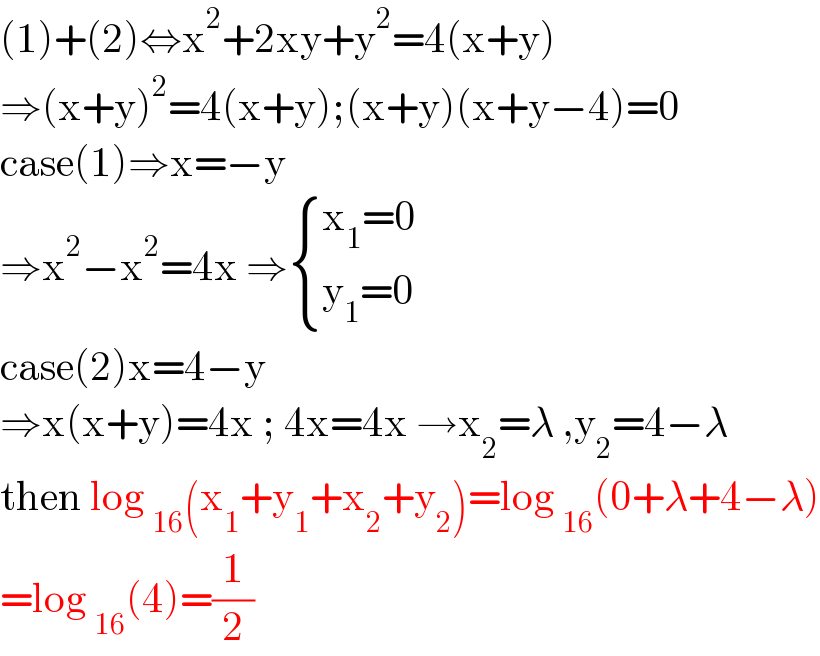
$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{x}+\mathrm{y}\right) \\ $$$$\Rightarrow\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{x}+\mathrm{y}\right);\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\Rightarrow\mathrm{x}=−\mathrm{y}\: \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} =\mathrm{4x}\:\Rightarrow\begin{cases}{\mathrm{x}_{\mathrm{1}} =\mathrm{0}}\\{\mathrm{y}_{\mathrm{1}} =\mathrm{0}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\mathrm{x}=\mathrm{4}−\mathrm{y} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{4x}\:;\:\mathrm{4x}=\mathrm{4x}\:\rightarrow\mathrm{x}_{\mathrm{2}} =\lambda\:,\mathrm{y}_{\mathrm{2}} =\mathrm{4}−\lambda \\ $$$$\mathrm{then}\:\mathrm{log}\:_{\mathrm{16}} \left(\mathrm{x}_{\mathrm{1}} +\mathrm{y}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +\mathrm{y}_{\mathrm{2}} \right)=\mathrm{log}\:_{\mathrm{16}} \left(\mathrm{0}+\lambda+\mathrm{4}−\lambda\right) \\ $$$$=\mathrm{log}\:_{\mathrm{16}} \left(\mathrm{4}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 02/Aug/21
$${Thank}\:{You}\:{Ser},\:{Cool} \\ $$
