Question Number 148756 by mathdanisur last updated on 30/Jul/21
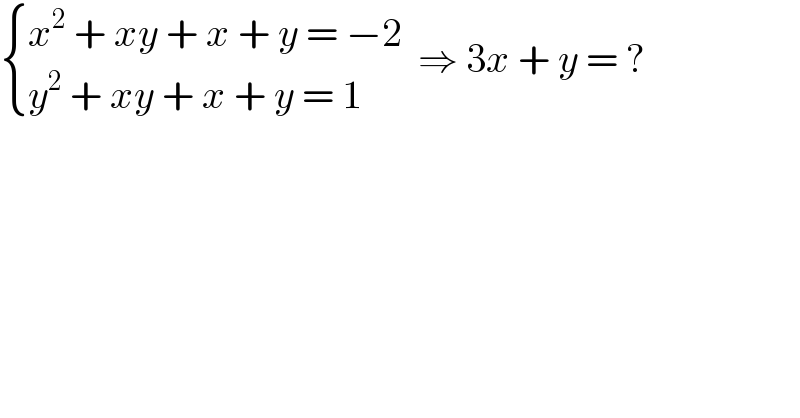
$$\begin{cases}{{x}^{\mathrm{2}} \:+\:{xy}\:+\:{x}\:+\:{y}\:=\:−\mathrm{2}}\\{{y}^{\mathrm{2}} \:+\:{xy}\:+\:{x}\:+\:{y}\:=\:\mathrm{1}}\end{cases}\:\:\Rightarrow\:\mathrm{3}{x}\:+\:{y}\:=\:? \\ $$
Answered by mindispower last updated on 30/Jul/21
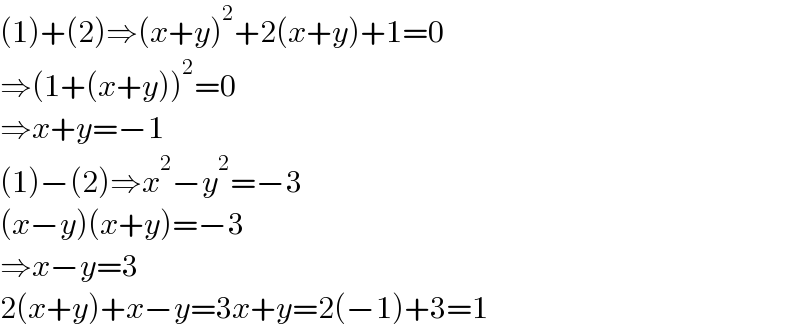
$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow\left({x}+{y}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+{y}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\left({x}+{y}\right)\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}+{y}=−\mathrm{1} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =−\mathrm{3} \\ $$$$\left({x}−{y}\right)\left({x}+{y}\right)=−\mathrm{3} \\ $$$$\Rightarrow{x}−{y}=\mathrm{3} \\ $$$$\mathrm{2}\left({x}+{y}\right)+{x}−{y}=\mathrm{3}{x}+{y}=\mathrm{2}\left(−\mathrm{1}\right)+\mathrm{3}=\mathrm{1} \\ $$
Commented by mathdanisur last updated on 31/Jul/21

$${Thank}\:{You}\:{Ser} \\ $$
