Question Number 49229 by munnabhai455111@gmail.com last updated on 04/Dec/18

$$\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} \\ $$
Commented by Abdo msup. last updated on 04/Dec/18
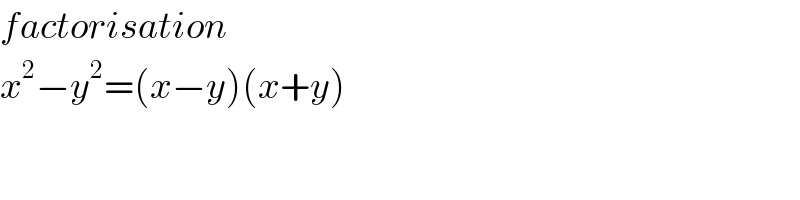
$${factorisation} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\left({x}−{y}\right)\left({x}+{y}\right) \\ $$
Commented by munnabhai455111@gmail.com last updated on 04/Dec/18
thanks
Commented by hknkrc46 last updated on 04/Dec/18
![=(x−y)(x+y) or =((√(x^4 −2x^2 y^2 +y^4 )) (∣x∣>∣y∣) or =((√x)−(√y))((√x)+(√y))[((√x)+(√y))^2 −2(√(xy))] (x,y≮0) =((√x)−(√y))((√x)+(√y))^3 −2(√(xy))((√x)−(√y)) (x,y≮0) =((√x)−(√y))((√x)+(√y))^3 −2x(√y)+2y(√x) (x,y≮0) or =(x−k)(x+k)−(y−k)(y+k) (k∈R) or =(x+(√y))(x−(√y))−[(y−(1/2))^2 −(1/4)] (y≮0)](https://www.tinkutara.com/question/Q49240.png)
$$=\left({x}−{y}\right)\left({x}+{y}\right) \\ $$$$\boldsymbol{{or}} \\ $$$$=\left(\sqrt{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} }\:\left(\mid{x}\mid>\mid{y}\mid\right)\right. \\ $$$$\boldsymbol{{or}} \\ $$$$=\left(\sqrt{{x}}−\sqrt{{y}}\right)\left(\sqrt{{x}}+\sqrt{{y}}\right)\left[\left(\sqrt{{x}}+\sqrt{{y}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{{xy}}\right]\:\left({x},{y}\nless\mathrm{0}\right) \\ $$$$=\left(\sqrt{{x}}−\sqrt{{y}}\right)\left(\sqrt{{x}}+\sqrt{{y}}\right)^{\mathrm{3}} −\mathrm{2}\sqrt{{xy}}\left(\sqrt{{x}}−\sqrt{{y}}\right)\:\left({x},{y}\nless\mathrm{0}\right) \\ $$$$=\left(\sqrt{{x}}−\sqrt{{y}}\right)\left(\sqrt{{x}}+\sqrt{{y}}\right)^{\mathrm{3}} −\mathrm{2}{x}\sqrt{{y}}+\mathrm{2}{y}\sqrt{{x}}\:\left({x},{y}\nless\mathrm{0}\right) \\ $$$$\boldsymbol{{or}} \\ $$$$=\left({x}−{k}\right)\left({x}+{k}\right)−\left({y}−{k}\right)\left({y}+{k}\right)\:\left({k}\in\mathbb{R}\right) \\ $$$$\boldsymbol{{or}} \\ $$$$=\left({x}+\sqrt{{y}}\right)\left({x}−\sqrt{{y}}\right)−\left[\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right]\:\left({y}\nless\mathrm{0}\right) \\ $$
Commented by Pk1167156@gmail.com last updated on 06/Dec/18
Very nice sir
