Question Number 105023 by bemath last updated on 25/Jul/20
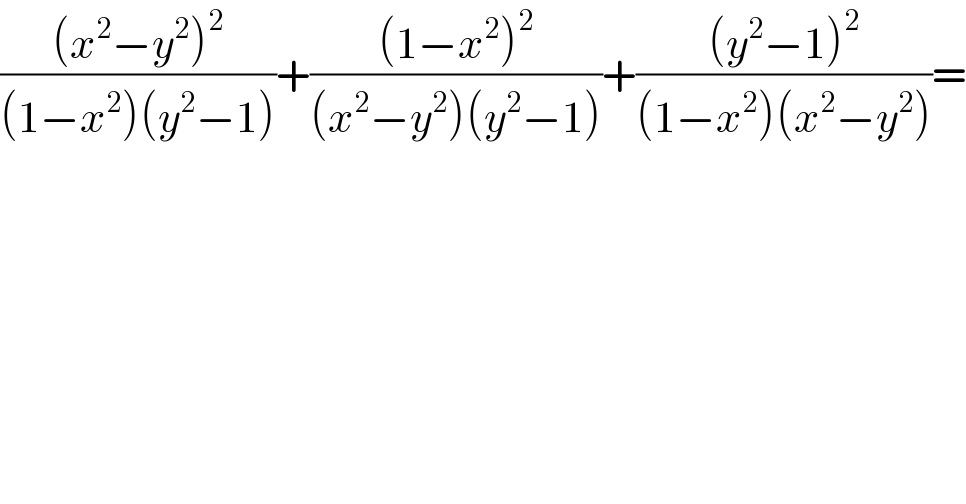
$$\frac{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}= \\ $$$$ \\ $$
Answered by john santu last updated on 25/Jul/20
![(((x^2 −y^2 )^3 +(1−x^2 )^3 +(y^2 −1)^3 )/((1−x^2 )(y^2 −1)(x^2 −y^2 ))) [ set (x^2 −y^2 ) = u ; (1−x^2 ) = v ; (y^2 −1) = w ] ⇔((u^3 +v^2 +w^3 )/(uvw)) = (((u+w)^3 −3uw(u+w)+v^3 )/(uvw)) [ u+w = x^2 −1 = −v ] ⇒((−v^3 +3uvw+v^3 )/(uvw)) = ((3uvw)/(uvw)) = 3 (JS ★♠)](https://www.tinkutara.com/question/Q105027.png)
$$\frac{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{3}} +\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)} \\ $$$$\left[\:{set}\:\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\:=\:{u}\:;\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:=\:{v}\:;\right. \\ $$$$\left.\left({y}^{\mathrm{2}} −\mathrm{1}\right)\:=\:{w}\:\right]\: \\ $$$$\Leftrightarrow\frac{{u}^{\mathrm{3}} +{v}^{\mathrm{2}} +{w}^{\mathrm{3}} }{{uvw}}\:=\:\frac{\left({u}+{w}\right)^{\mathrm{3}} −\mathrm{3}{uw}\left({u}+{w}\right)+{v}^{\mathrm{3}} }{{uvw}} \\ $$$$\left[\:{u}+{w}\:=\:{x}^{\mathrm{2}} −\mathrm{1}\:=\:−{v}\:\right] \\ $$$$\Rightarrow\frac{−{v}^{\mathrm{3}} +\mathrm{3}{uvw}+{v}^{\mathrm{3}} }{{uvw}}\:=\:\frac{\mathrm{3}{uvw}}{{uvw}}\:=\:\mathrm{3} \\ $$$$\left({JS}\:\bigstar\spadesuit\right) \\ $$
