Question Number 148324 by Odhiambojr last updated on 27/Jul/21

$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{3},\:{find}\:{dy}/{dx} \\ $$
Answered by liberty last updated on 27/Jul/21
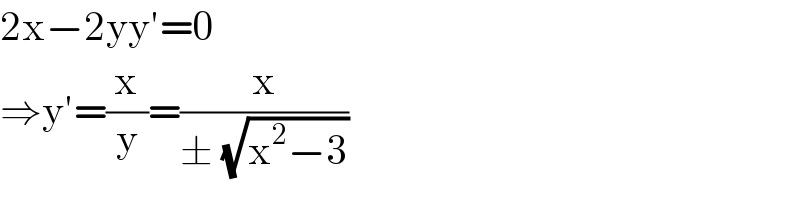
$$\mathrm{2x}−\mathrm{2yy}'=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}'=\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{x}}{\pm\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}}\: \\ $$
Answered by mathmax by abdo last updated on 27/Jul/21

$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}\:} \:=\mathrm{3}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}=\mathrm{y}^{\mathrm{2}} \:\Rightarrow\mathrm{y}=\overset{−} {+}\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\overset{−} {+}\frac{\mathrm{2x}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}}=\overset{−} {+}\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}}} \\ $$
