Question Number 163632 by HongKing last updated on 08/Jan/22
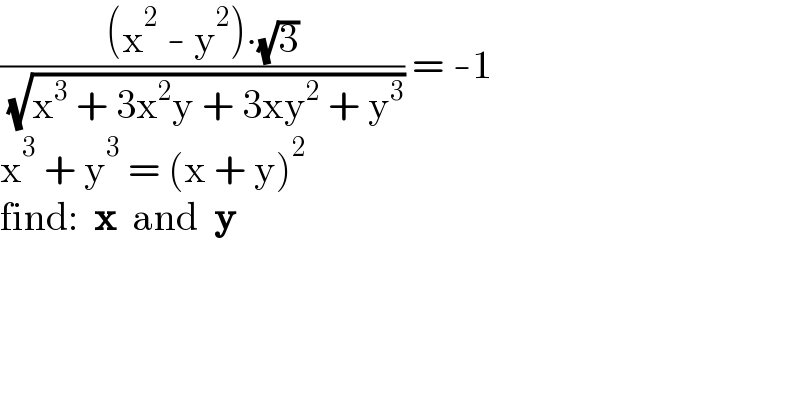
$$\frac{\left(\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{y}^{\mathrm{2}} \right)\centerdot\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{3x}^{\mathrm{2}} \mathrm{y}\:+\:\mathrm{3xy}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{3}} }}\:=\:-\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{3}} \:=\:\left(\mathrm{x}\:+\:\mathrm{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{find}:\:\:\boldsymbol{\mathrm{x}}\:\:\mathrm{and}\:\:\boldsymbol{\mathrm{y}} \\ $$
Answered by MJS_new last updated on 08/Jan/22
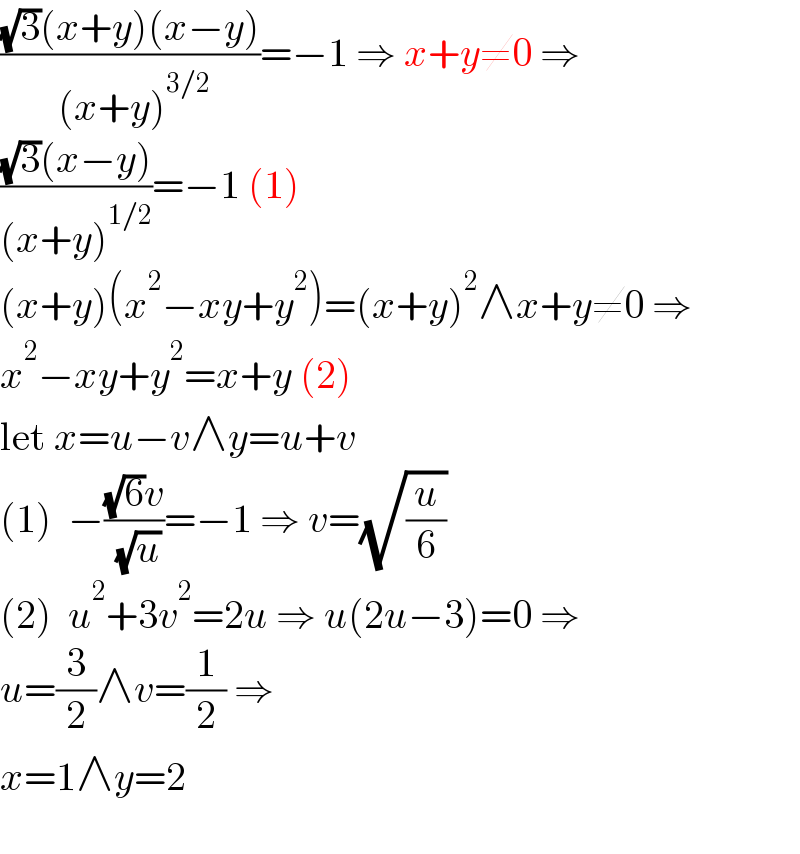
$$\frac{\sqrt{\mathrm{3}}\left({x}+{y}\right)\left({x}−{y}\right)}{\:\left({x}+{y}\right)^{\mathrm{3}/\mathrm{2}} }=−\mathrm{1}\:\Rightarrow\:{x}+{y}\neq\mathrm{0}\:\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{3}}\left({x}−{y}\right)}{\left({x}+{y}\right)^{\mathrm{1}/\mathrm{2}} }=−\mathrm{1}\:\left(\mathrm{1}\right) \\ $$$$\left({x}+{y}\right)\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)=\left({x}+{y}\right)^{\mathrm{2}} \wedge{x}+{y}\neq\mathrm{0}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} ={x}+{y}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{let}\:{x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\left(\mathrm{1}\right)\:\:−\frac{\sqrt{\mathrm{6}}{v}}{\:\sqrt{{u}}}=−\mathrm{1}\:\Rightarrow\:{v}=\sqrt{\frac{{u}}{\mathrm{6}}} \\ $$$$\left(\mathrm{2}\right)\:\:{u}^{\mathrm{2}} +\mathrm{3}{v}^{\mathrm{2}} =\mathrm{2}{u}\:\Rightarrow\:{u}\left(\mathrm{2}{u}−\mathrm{3}\right)=\mathrm{0}\:\Rightarrow \\ $$$${u}=\frac{\mathrm{3}}{\mathrm{2}}\wedge{v}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${x}=\mathrm{1}\wedge{y}=\mathrm{2} \\ $$$$ \\ $$
Commented by HongKing last updated on 09/Jan/22
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Answered by behi834171 last updated on 09/Jan/22
![x+y≠0 let:x+y=p ,xy=q ⇒(((√3)(x^2 −y^2 ))/((x+y)^(3/2) ))=−1⇒(((√3)(x−y))/((x+y)^(1/2) ))=−1⇒ ((3(x^2 +y^2 −2xy))/(x+y))=1⇒3(p^2 −4q)=p⇒ { ((3p^2 −12q−p=0)),((p^2 −3q−p=0)) :}⇒−p^2 +3p=0⇒ { ((p=0[×])),((p=3[ok])) :} p=3⇒9−3q−3=0⇒q=2⇒[p=3,q=2] ⇒ { ((x+y=3)),((xy=2)) :}⇒(x,y)=(1,2) .■](https://www.tinkutara.com/question/Q163639.png)
$${x}+{y}\neq\mathrm{0}\:{let}:\boldsymbol{{x}}+\boldsymbol{{y}}=\boldsymbol{{p}}\:,\boldsymbol{{xy}}=\boldsymbol{{q}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}{\left({x}+{y}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=−\mathrm{1}\Rightarrow\frac{\sqrt{\mathrm{3}}\left({x}−{y}\right)}{\left({x}+{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }=−\mathrm{1}\Rightarrow \\ $$$$\frac{\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}\right)}{{x}+{y}}=\mathrm{1}\Rightarrow\mathrm{3}\left({p}^{\mathrm{2}} −\mathrm{4}{q}\right)={p}\Rightarrow \\ $$$$\begin{cases}{\mathrm{3}{p}^{\mathrm{2}} −\mathrm{12}{q}−{p}=\mathrm{0}}\\{{p}^{\mathrm{2}} −\mathrm{3}{q}−{p}=\mathrm{0}}\end{cases}\Rightarrow−{p}^{\mathrm{2}} +\mathrm{3}{p}=\mathrm{0}\Rightarrow\begin{cases}{{p}=\mathrm{0}\left[×\right]}\\{{p}=\mathrm{3}\left[{ok}\right]}\end{cases} \\ $$$${p}=\mathrm{3}\Rightarrow\mathrm{9}−\mathrm{3}{q}−\mathrm{3}=\mathrm{0}\Rightarrow{q}=\mathrm{2}\Rightarrow\left[{p}=\mathrm{3},{q}=\mathrm{2}\right] \\ $$$$\Rightarrow\begin{cases}{{x}+{y}=\mathrm{3}}\\{{xy}=\mathrm{2}}\end{cases}\Rightarrow\left({x},{y}\right)=\left(\mathrm{1},\mathrm{2}\right)\:.\blacksquare \\ $$
Commented by MJS_new last updated on 09/Jan/22

$$\mathrm{with}\:{x}=\mathrm{2}\wedge{y}=\mathrm{1}\:\mathrm{the}\:\mathrm{first}\:\mathrm{original}\:\mathrm{equation} \\ $$$$\mathrm{is}\:\mathrm{false} \\ $$
Commented by behi834171 last updated on 09/Jan/22
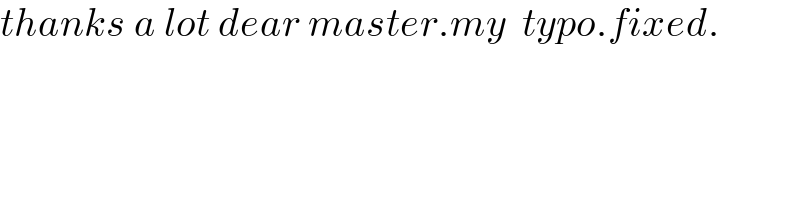
$${thanks}\:{a}\:{lot}\:{dear}\:{master}.{my}\:\:{typo}.{fixed}. \\ $$
Commented by MJS_new last updated on 09/Jan/22

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}! \\ $$
