Question Number 95449 by bobhans last updated on 25/May/20
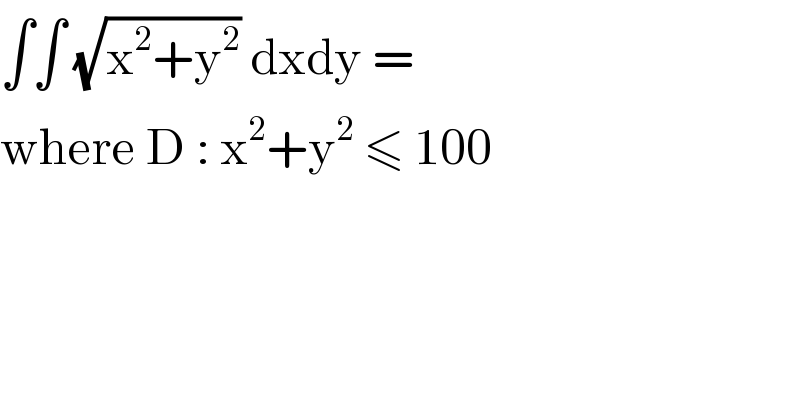
$$\int\int\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\mathrm{dxdy}\:=\: \\ $$$$\mathrm{where}\:\mathrm{D}\::\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:\leqslant\:\mathrm{100}\: \\ $$
Commented by mr W last updated on 25/May/20

$$=\int_{\mathrm{0}} ^{\mathrm{10}} \int_{\mathrm{0}} ^{\mathrm{2}\pi} {r}^{\mathrm{2}} {d}\theta{dr} \\ $$$$=\mathrm{2}\pi×\frac{\mathrm{10}^{\mathrm{3}} }{\mathrm{3}}=\frac{\mathrm{2000}\pi}{\mathrm{3}} \\ $$
Commented by bobhans last updated on 25/May/20
$$\mathrm{i}\:\mathrm{have}\:\mathrm{2}\:\:\mathrm{different}\:\mathrm{answers} \\ $$
Commented by mr W last updated on 25/May/20

$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }={r} \\ $$$${dxdy}={rd}\theta{dr} \\ $$$$\Rightarrow{I}=\int\int{r}^{\mathrm{2}} {drd}\theta=… \\ $$
Commented by john santu last updated on 25/May/20
who deleted my answer without confirmation?
Commented by mr W last updated on 25/May/20

$${are}\:{you}\:{sure}\:{you}\:{didn}'{t}\:{delete}\:{it}\:{by} \\ $$$${accident}? \\ $$$${the}\:{same}\:{happend}\:{to}\:{me}\:{once},\:{i}\:{was} \\ $$$${sure}.\:{but}\:{the}\:{developer}\:{said}\:{that}\:{this} \\ $$$${is}\:{impossible}.\:{please}\:{report}\:{this}\:{issue} \\ $$$${to}\:{him}\:{so}\:{that}\:{i}\:{am}\:{not}\:{the}\:{only}\:{one} \\ $$$${who}\:{reported}\:{this}\:{issue}. \\ $$
Commented by john santu last updated on 25/May/20
Yes, I am sure. I have nothing to delete that answer. I confirm to the admin
Commented by Tinku Tara last updated on 25/May/20
Strictly Technically speaking: It is not impossible to lose a post if database crashed and older snapshot is restored then a bunch of post might not be present. So far we did not come across this issue. Individual record corruptions are very unlikely but we will continue to monitor. will add more logs on server.
We will also delete flagged posts and other junk posts/blank posts etc periodically to keep the forum clean. Depending upon workload it might be a few days before we clear. This process is manual.
Also post/screenshots specifically directed towards us to us for problem/suggestions are removed.
If any images/links are flagged we will remove. Any discussion on app ( inclduing about this app) are also removed periodically once the discussion is understood.
Answered by mathmax by abdo last updated on 25/May/20
![we use the diffeomorphism x =10r cosθ and y =10r sinθ ⇒ ∫∫ (√(x^2 +y^2 ))dxdy =∫_0 ^1 ∫_(−π) ^π (10r)100r dr dθ =1000 ∫_0 ^1 (r^2 dr)(2π) =2000π [(r^3 /3)]_0 ^1 =((2000π)/3)](https://www.tinkutara.com/question/Q95476.png)
$$\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{diffeomorphism}\:\mathrm{x}\:=\mathrm{10r}\:\mathrm{cos}\theta\:\mathrm{and}\:\mathrm{y}\:=\mathrm{10r}\:\mathrm{sin}\theta \\ $$$$\Rightarrow\:\int\int\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} }\mathrm{dxdy}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{−\pi} ^{\pi} \:\left(\mathrm{10r}\right)\mathrm{100r}\:\mathrm{dr}\:\mathrm{d}\theta \\ $$$$=\mathrm{1000}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{r}^{\mathrm{2}} \:\mathrm{dr}\right)\left(\mathrm{2}\pi\right)\:=\mathrm{2000}\pi\:\left[\frac{\mathrm{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{2000}\pi}{\mathrm{3}} \\ $$
