Question Number 14211 by prakash jain last updated on 29/May/17
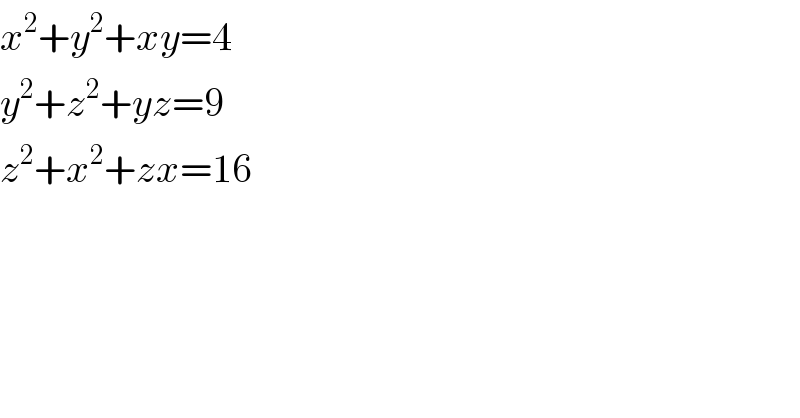
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}=\mathrm{4} \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{yz}=\mathrm{9} \\ $$$${z}^{\mathrm{2}} +{x}^{\mathrm{2}} +{zx}=\mathrm{16} \\ $$
Commented by prakash jain last updated on 29/May/17
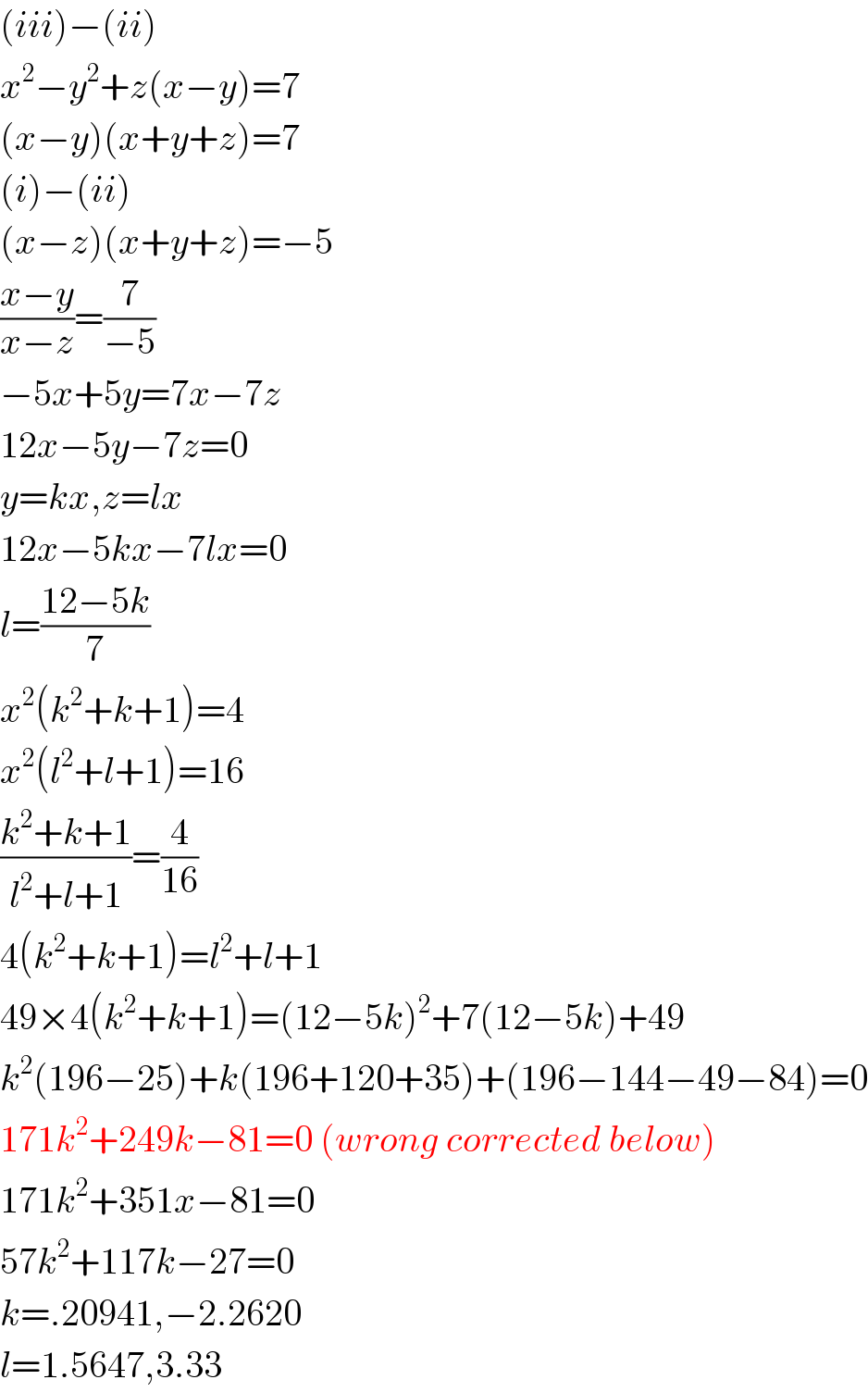
$$\left({iii}\right)−\left({ii}\right) \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{z}\left({x}−{y}\right)=\mathrm{7} \\ $$$$\left({x}−{y}\right)\left({x}+{y}+{z}\right)=\mathrm{7} \\ $$$$\left({i}\right)−\left({ii}\right) \\ $$$$\left({x}−{z}\right)\left({x}+{y}+{z}\right)=−\mathrm{5} \\ $$$$\frac{{x}−{y}}{{x}−{z}}=\frac{\mathrm{7}}{−\mathrm{5}} \\ $$$$−\mathrm{5}{x}+\mathrm{5}{y}=\mathrm{7}{x}−\mathrm{7}{z} \\ $$$$\mathrm{12}{x}−\mathrm{5}{y}−\mathrm{7}{z}=\mathrm{0} \\ $$$${y}={kx},{z}={lx} \\ $$$$\mathrm{12}{x}−\mathrm{5}{kx}−\mathrm{7}{lx}=\mathrm{0} \\ $$$${l}=\frac{\mathrm{12}−\mathrm{5}{k}}{\mathrm{7}} \\ $$$${x}^{\mathrm{2}} \left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)=\mathrm{4} \\ $$$${x}^{\mathrm{2}} \left({l}^{\mathrm{2}} +{l}+\mathrm{1}\right)=\mathrm{16} \\ $$$$\frac{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{{l}^{\mathrm{2}} +{l}+\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{16}} \\ $$$$\mathrm{4}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)={l}^{\mathrm{2}} +{l}+\mathrm{1} \\ $$$$\mathrm{49}×\mathrm{4}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)=\left(\mathrm{12}−\mathrm{5}{k}\right)^{\mathrm{2}} +\mathrm{7}\left(\mathrm{12}−\mathrm{5}{k}\right)+\mathrm{49} \\ $$$${k}^{\mathrm{2}} \left(\mathrm{196}−\mathrm{25}\right)+{k}\left(\mathrm{196}+\mathrm{120}+\mathrm{35}\right)+\left(\mathrm{196}−\mathrm{144}−\mathrm{49}−\mathrm{84}\right)=\mathrm{0} \\ $$$$\mathrm{171}{k}^{\mathrm{2}} +\mathrm{249}{k}−\mathrm{81}=\mathrm{0}\:\left({wrong}\:{corrected}\:{below}\right) \\ $$$$\mathrm{171}{k}^{\mathrm{2}} +\mathrm{351}{x}−\mathrm{81}=\mathrm{0} \\ $$$$\mathrm{57}{k}^{\mathrm{2}} +\mathrm{117}{k}−\mathrm{27}=\mathrm{0} \\ $$$${k}=.\mathrm{20941},−\mathrm{2}.\mathrm{2620} \\ $$$${l}=\mathrm{1}.\mathrm{5647},\mathrm{3}.\mathrm{33} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
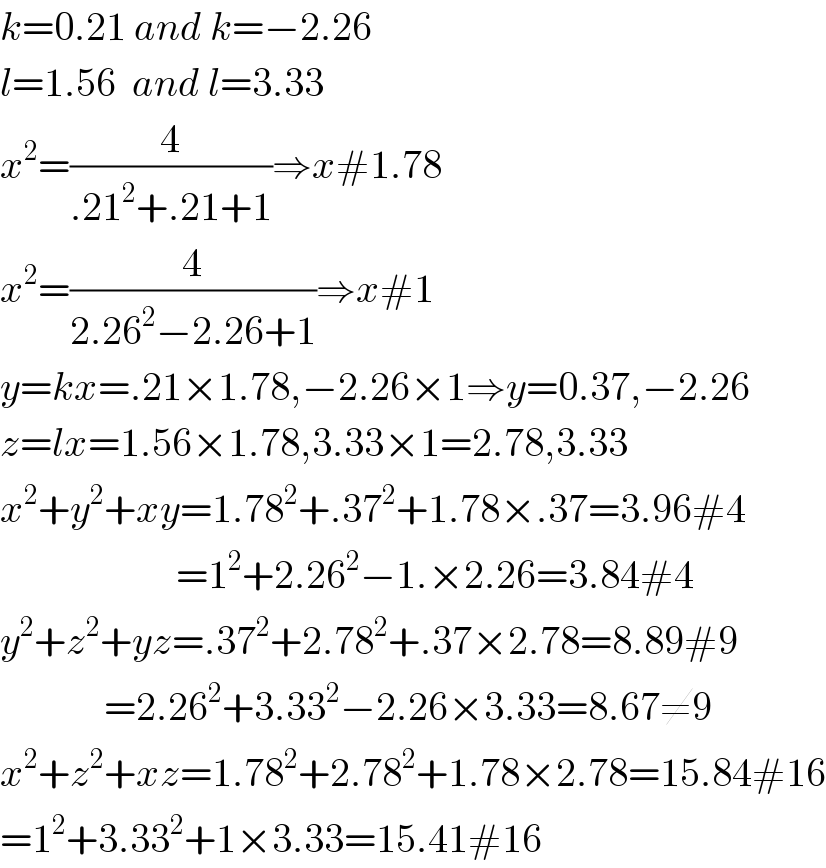
$${k}=\mathrm{0}.\mathrm{21}\:{and}\:{k}=−\mathrm{2}.\mathrm{26} \\ $$$${l}=\mathrm{1}.\mathrm{56}\:\:{and}\:{l}=\mathrm{3}.\mathrm{33} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{4}}{.\mathrm{21}^{\mathrm{2}} +.\mathrm{21}+\mathrm{1}}\Rightarrow{x}#\mathrm{1}.\mathrm{78} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{2}.\mathrm{26}^{\mathrm{2}} −\mathrm{2}.\mathrm{26}+\mathrm{1}}\Rightarrow{x}#\mathrm{1} \\ $$$${y}={kx}=.\mathrm{21}×\mathrm{1}.\mathrm{78},−\mathrm{2}.\mathrm{26}×\mathrm{1}\Rightarrow{y}=\mathrm{0}.\mathrm{37},−\mathrm{2}.\mathrm{26} \\ $$$${z}={lx}=\mathrm{1}.\mathrm{56}×\mathrm{1}.\mathrm{78},\mathrm{3}.\mathrm{33}×\mathrm{1}=\mathrm{2}.\mathrm{78},\mathrm{3}.\mathrm{33} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}=\mathrm{1}.\mathrm{78}^{\mathrm{2}} +.\mathrm{37}^{\mathrm{2}} +\mathrm{1}.\mathrm{78}×.\mathrm{37}=\mathrm{3}.\mathrm{96}#\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}^{\mathrm{2}} +\mathrm{2}.\mathrm{26}^{\mathrm{2}} −\mathrm{1}.×\mathrm{2}.\mathrm{26}=\mathrm{3}.\mathrm{84}#\mathrm{4} \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{yz}=.\mathrm{37}^{\mathrm{2}} +\mathrm{2}.\mathrm{78}^{\mathrm{2}} +.\mathrm{37}×\mathrm{2}.\mathrm{78}=\mathrm{8}.\mathrm{89}#\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}.\mathrm{26}^{\mathrm{2}} +\mathrm{3}.\mathrm{33}^{\mathrm{2}} −\mathrm{2}.\mathrm{26}×\mathrm{3}.\mathrm{33}=\mathrm{8}.\mathrm{67}\neq\mathrm{9} \\ $$$${x}^{\mathrm{2}} +{z}^{\mathrm{2}} +{xz}=\mathrm{1}.\mathrm{78}^{\mathrm{2}} +\mathrm{2}.\mathrm{78}^{\mathrm{2}} +\mathrm{1}.\mathrm{78}×\mathrm{2}.\mathrm{78}=\mathrm{15}.\mathrm{84}#\mathrm{16} \\ $$$$=\mathrm{1}^{\mathrm{2}} +\mathrm{3}.\mathrm{33}^{\mathrm{2}} +\mathrm{1}×\mathrm{3}.\mathrm{33}=\mathrm{15}.\mathrm{41}#\mathrm{16} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
Commented by prakash jain last updated on 29/May/17
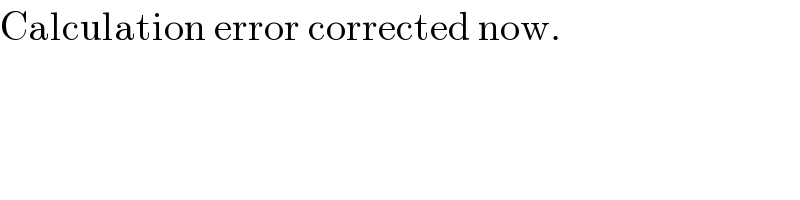
$$\mathrm{Calculation}\:\mathrm{error}\:\mathrm{corrected}\:\mathrm{now}. \\ $$
Commented by prakash jain last updated on 29/May/17

$${k}=.\mathrm{20941},{l}=\mathrm{1}.\mathrm{5647} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{4}}{\left(.\mathrm{2094}\right)^{\mathrm{2}} +\left(.\mathrm{2094}\right)+\mathrm{1}} \\ $$$${x}=\pm\mathrm{1}.\mathrm{78653} \\ $$$${y}=\pm.\mathrm{37411} \\ $$$${z}=\pm\mathrm{1}.\mathrm{5647}×\mathrm{1}.\mathrm{78653}=\pm\mathrm{2}.\mathrm{7954} \\ $$$${k}=−\mathrm{2}.\mathrm{262},{l}=\mathrm{3}.\mathrm{33} \\ $$$${x}=\pm\mathrm{1}.\mathrm{01866} \\ $$$${y}=\mp\mathrm{2}.\mathrm{30525} \\ $$$${z}=\pm\mathrm{3}.\mathrm{39217} \\ $$
Commented by prakash jain last updated on 29/May/17

$$\mathrm{Check}\:\mathrm{few}\:\mathrm{combination}\:\mathrm{with} \\ $$$$\mathrm{calculator}\:\mathrm{answers}\:\mathrm{are}\:\mathrm{correct}\:\mathrm{now}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

$${thank}\:{you}\:{mr}\:{prakash}. \\ $$$${have}\:{any}\:{idea}\:{for}\:{general}\:{solutions}? \\ $$
Commented by prakash jain last updated on 30/May/17
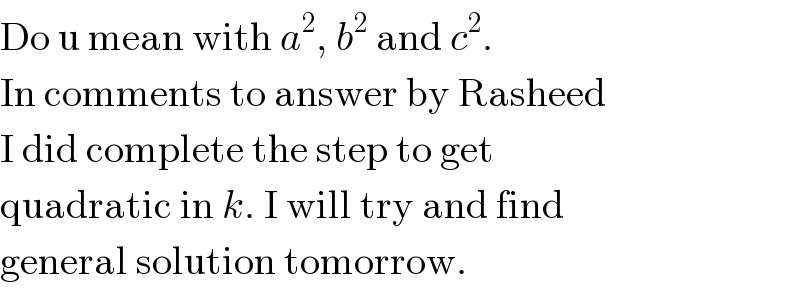
$$\mathrm{Do}\:\mathrm{u}\:\mathrm{mean}\:\mathrm{with}\:{a}^{\mathrm{2}} ,\:{b}^{\mathrm{2}} \:\mathrm{and}\:{c}^{\mathrm{2}} . \\ $$$$\mathrm{In}\:\mathrm{comments}\:\mathrm{to}\:\mathrm{answer}\:\mathrm{by}\:\mathrm{Rasheed} \\ $$$$\mathrm{I}\:\mathrm{did}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{step}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{quadratic}\:\mathrm{in}\:{k}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{try}\:\mathrm{and}\:\mathrm{find} \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{tomorrow}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

$${thank}\:{you}\:{my}\:{dear}\:{friend}.{i}\:{will}\:{pray} \\ $$$${for}\:{your}\:{succses}.{you}\:{can}\:{do}\:{it}. \\ $$
Commented by ajfour last updated on 30/May/17
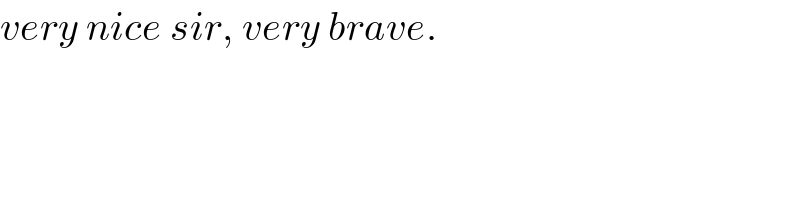
$${very}\:{nice}\:{sir},\:{very}\:{brave}. \\ $$
Commented by Tawa11 last updated on 15/Jan/22

$$\mathrm{Nice}\:\mathrm{sir} \\ $$
