Question Number 154099 by EDWIN88 last updated on 14/Sep/21
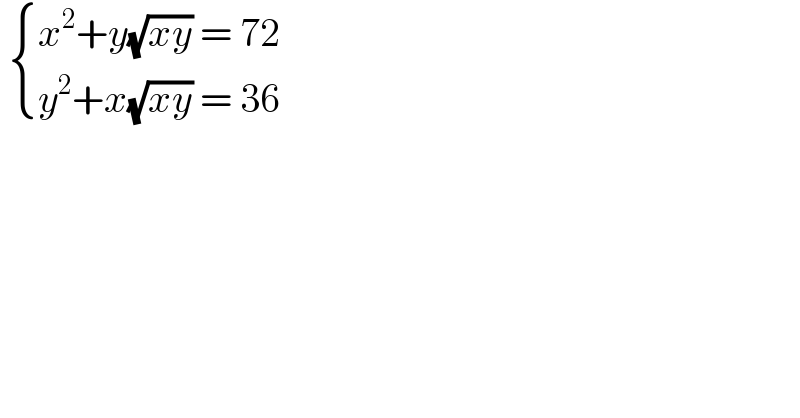
$$\:\begin{cases}{{x}^{\mathrm{2}} +{y}\sqrt{{xy}}\:=\:\mathrm{72}}\\{{y}^{\mathrm{2}} +{x}\sqrt{{xy}}\:=\:\mathrm{36}}\end{cases} \\ $$
Answered by EDWIN88 last updated on 14/Sep/21
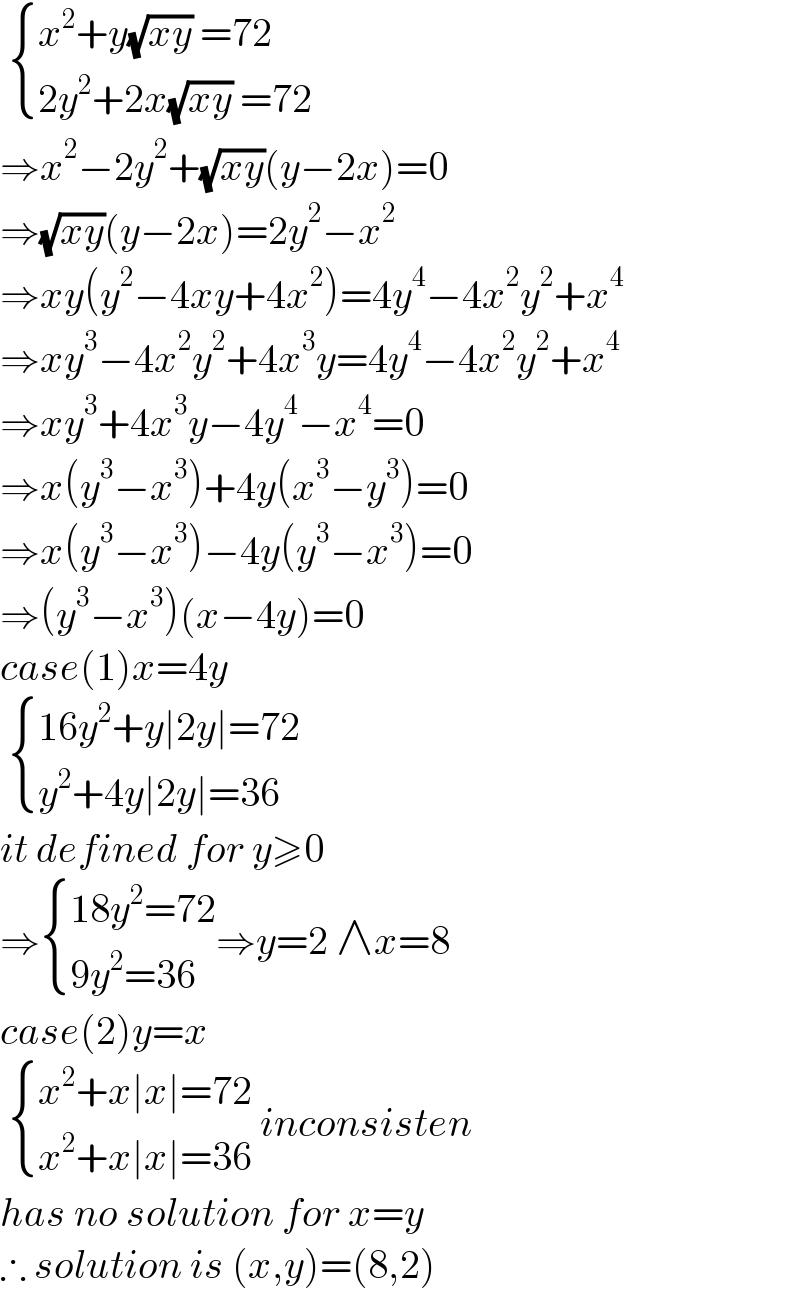
$$\:\begin{cases}{{x}^{\mathrm{2}} +{y}\sqrt{{xy}}\:=\mathrm{72}}\\{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{x}\sqrt{{xy}}\:=\mathrm{72}}\end{cases} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} +\sqrt{{xy}}\left({y}−\mathrm{2}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{xy}}\left({y}−\mathrm{2}{x}\right)=\mathrm{2}{y}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$$\Rightarrow{xy}\left({y}^{\mathrm{2}} −\mathrm{4}{xy}+\mathrm{4}{x}^{\mathrm{2}} \right)=\mathrm{4}{y}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{x}^{\mathrm{4}} \\ $$$$\Rightarrow{xy}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} {y}=\mathrm{4}{y}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{x}^{\mathrm{4}} \\ $$$$\Rightarrow{xy}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{3}} {y}−\mathrm{4}{y}^{\mathrm{4}} −{x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow{x}\left({y}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)+\mathrm{4}{y}\left({x}^{\mathrm{3}} −{y}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\Rightarrow{x}\left({y}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)−\mathrm{4}{y}\left({y}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left({y}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)\left({x}−\mathrm{4}{y}\right)=\mathrm{0} \\ $$$${case}\left(\mathrm{1}\right){x}=\mathrm{4}{y} \\ $$$$\:\begin{cases}{\mathrm{16}{y}^{\mathrm{2}} +{y}\mid\mathrm{2}{y}\mid=\mathrm{72}}\\{{y}^{\mathrm{2}} +\mathrm{4}{y}\mid\mathrm{2}{y}\mid=\mathrm{36}}\end{cases} \\ $$$${it}\:{defined}\:{for}\:{y}\geqslant\mathrm{0}\: \\ $$$$\Rightarrow\begin{cases}{\mathrm{18}{y}^{\mathrm{2}} =\mathrm{72}}\\{\mathrm{9}{y}^{\mathrm{2}} =\mathrm{36}}\end{cases}\Rightarrow{y}=\mathrm{2}\:\wedge{x}=\mathrm{8} \\ $$$${case}\left(\mathrm{2}\right){y}={x} \\ $$$$\:\begin{cases}{{x}^{\mathrm{2}} +{x}\mid{x}\mid=\mathrm{72}}\\{{x}^{\mathrm{2}} +{x}\mid{x}\mid=\mathrm{36}}\end{cases}\:{inconsisten} \\ $$$${has}\:{no}\:{solution}\:{for}\:{x}={y} \\ $$$$\therefore\:{solution}\:{is}\:\left({x},{y}\right)=\left(\mathrm{8},\mathrm{2}\right) \\ $$
Commented by Tawa11 last updated on 15/Sep/21

$$\mathrm{nice} \\ $$
