Question Number 130830 by Ar Brandon last updated on 29/Jan/21
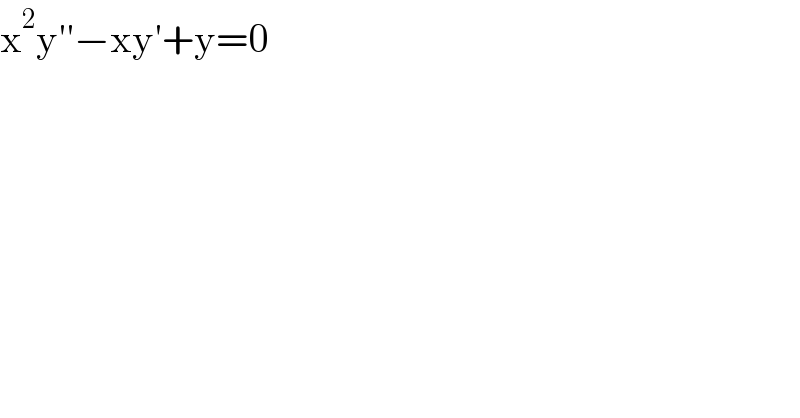
$$\mathrm{x}^{\mathrm{2}} \mathrm{y}''−\mathrm{xy}'+\mathrm{y}=\mathrm{0} \\ $$
Answered by bemath last updated on 29/Jan/21
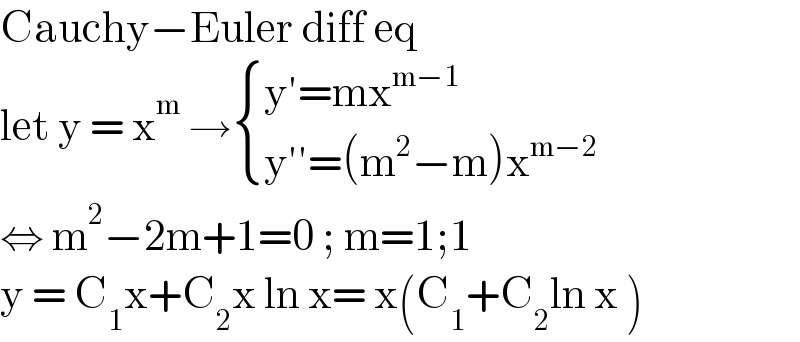
$$\mathrm{Cauchy}−\mathrm{Euler}\:\mathrm{diff}\:\mathrm{eq} \\ $$$$\mathrm{let}\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{m}} \:\rightarrow\begin{cases}{\mathrm{y}'=\mathrm{mx}^{\mathrm{m}−\mathrm{1}} }\\{\mathrm{y}''=\left(\mathrm{m}^{\mathrm{2}} −\mathrm{m}\right)\mathrm{x}^{\mathrm{m}−\mathrm{2}} }\end{cases} \\ $$$$\Leftrightarrow\:\mathrm{m}^{\mathrm{2}} −\mathrm{2m}+\mathrm{1}=\mathrm{0}\:;\:\mathrm{m}=\mathrm{1};\mathrm{1} \\ $$$$\mathrm{y}\:=\:\mathrm{C}_{\mathrm{1}} \mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{x}\:\mathrm{ln}\:\mathrm{x}=\:\mathrm{x}\left(\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \mathrm{ln}\:\mathrm{x}\:\right) \\ $$
