Question Number 185728 by aba last updated on 26/Jan/23

$$\left(\mathrm{x}−\mathrm{2013}\right)!=\mathrm{6}!\mathrm{7}! \\ $$$$\mathrm{x}=?? \\ $$
Answered by mr W last updated on 26/Jan/23
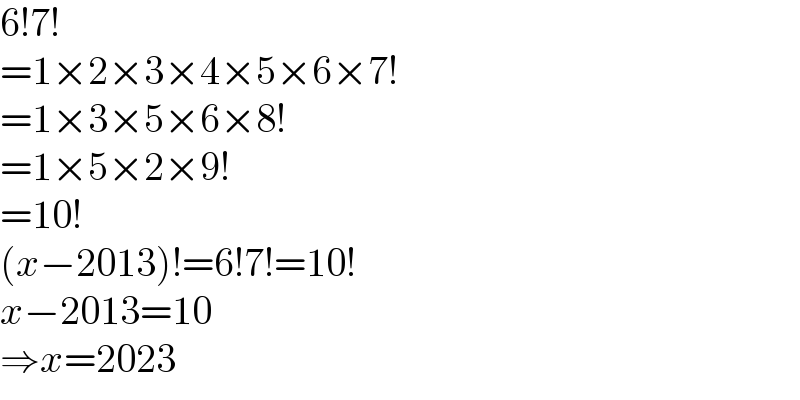
$$\mathrm{6}!\mathrm{7}! \\ $$$$=\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}×\mathrm{6}×\mathrm{7}! \\ $$$$=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{6}×\mathrm{8}! \\ $$$$=\mathrm{1}×\mathrm{5}×\mathrm{2}×\mathrm{9}! \\ $$$$=\mathrm{10}! \\ $$$$\left({x}−\mathrm{2013}\right)!=\mathrm{6}!\mathrm{7}!=\mathrm{10}! \\ $$$${x}−\mathrm{2013}=\mathrm{10} \\ $$$$\Rightarrow{x}=\mathrm{2023} \\ $$
Commented by Frix last updated on 27/Jan/23
![Is there another pair (m, n) with n!(n+1)!=m! except the trivial ones? Or maybe n!(n+k)!=m! [m, n, k ∈N]](https://www.tinkutara.com/question/Q185758.png)
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{another}\:\mathrm{pair}\:\left({m},\:{n}\right)\:\mathrm{with} \\ $$$${n}!\left({n}+\mathrm{1}\right)!={m}! \\ $$$$\mathrm{except}\:\mathrm{the}\:\mathrm{trivial}\:\mathrm{ones}? \\ $$$$\mathrm{Or}\:\mathrm{maybe}\:{n}!\left({n}+{k}\right)!={m}! \\ $$$$\left[{m},\:{n},\:{k}\:\in\mathbb{N}\right] \\ $$
