Menu Close

x-2ab-a-b-then-prove-that-x-a-x-a-x-b-x-b-2-

Tinku Tara 0 Comments
Pin




Question Number 185876 by MATHEMATICSAM last updated on 29/Jan/23
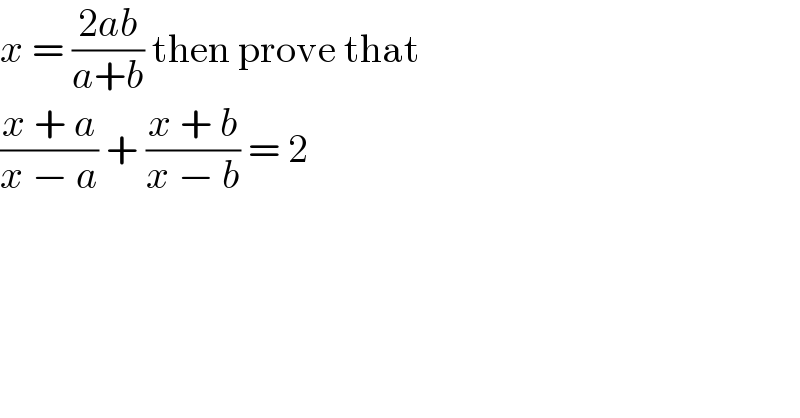
x = ((2ab)/(a+b)) then prove that ((x + a)/(x − a)) + ((x + b)/(x − b)) = 2
x=2aba+bthenprovethatx+ax−a+x+bx−b=2
Answered by Rasheed.Sindhi last updated on 29/Jan/23
x = ((2ab)/(a+b)) then prove that ((x + a)/(x − a)) + ((x + b)/(x − b)) = 2 LHS: =((x + a)/(x − a))−1 + ((x + b)/(x − b))−1+2 =((2a)/(x−a))+((2b)/(x−b))+2 =((2a)/(((2ab)/(a+b))−a))+((2b)/(((2ab)/(a+b))−b))+2 =((2a)/((2ab−a^2 −ab)/(a+b)))+((2b)/((2ab−ab−b^2 )/(a+b)))+2 =(2/((b−a)/(a+b)))+(2/((a−b)/(a+b)))+2 =−((2(a+b))/(a−b))+((2(a+b))/(a−b))+2 =2=RHS Proved
x=2aba+bthenprovethatx+ax−a+x+bx−b=2LHS:=x+ax−a−1+x+bx−b−1+2=2ax−a+2bx−b+2=2a2aba+b−a+2b2aba+b−b+2=2a2ab−a2−aba+b+2b2ab−ab−b2a+b+2=2b−aa+b+2a−ba+b+2=−2(a+b)a−b+2(a+b)a−b+2=2=RHSProved
Answered by ajfour last updated on 29/Jan/23
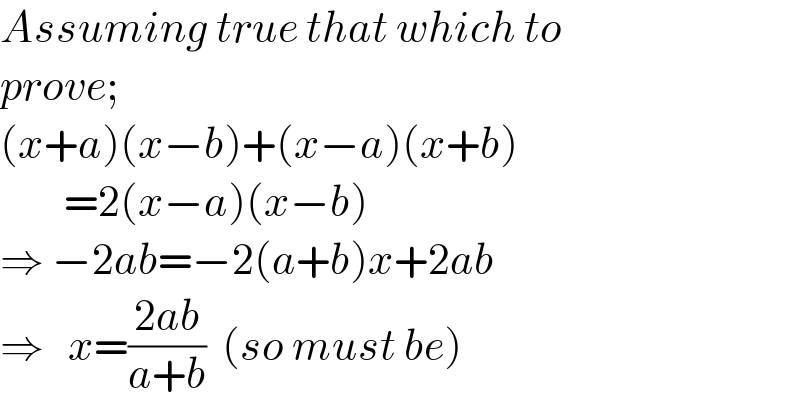
Assuming true that which to prove; (x+a)(x−b)+(x−a)(x+b) =2(x−a)(x−b) ⇒ −2ab=−2(a+b)x+2ab ⇒ x=((2ab)/(a+b)) (so must be)
Assumingtruethatwhichtoprove;(x+a)(x−b)+(x−a)(x+b)=2(x−a)(x−b)⇒−2ab=−2(a+b)x+2ab⇒x=2aba+b(somustbe)
Answered by HeferH last updated on 29/Jan/23
i. x(a +b) = 2ab ii. ((x + a)/(x −a)) + ((x + b)/(x − b)) = 2 + 2((a/(x − a)) + (b/(x − b))) = 2 + 2[((a(x−b) + b(x−a))/((x−a)(x−b)))] = 2 + 2[((x(a+b)−2ab)/((x−a)(x−b)))] = 2 + 2[(0/((x−a)(x−b)))] = 2 + 2(0) = 2 ✓
i.x(a+b)=2abii.x+ax−a+x+bx−b=2+2(ax−a+bx−b)=2+2[a(x−b)+b(x−a)(x−a)(x−b)]=2+2[x(a+b)−2ab(x−a)(x−b)]=2+2[0(x−a)(x−b)]=2+2(0)=2✓

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *