Question Number 85774 by M±th+et£s last updated on 24/Mar/20
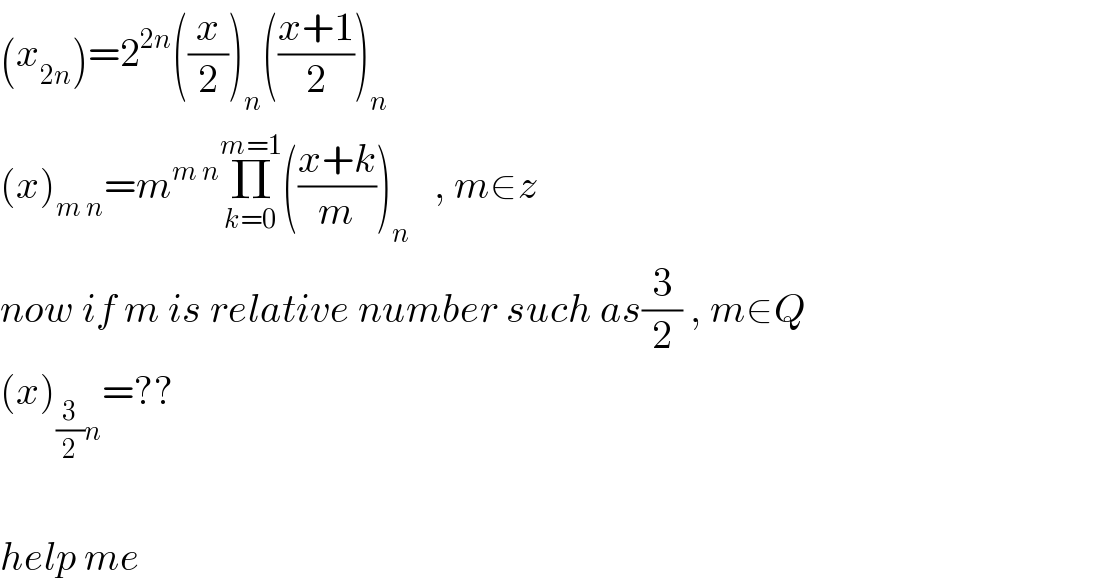
$$\left({x}_{\mathrm{2}{n}} \right)=\mathrm{2}^{\mathrm{2}{n}} \left(\frac{{x}}{\mathrm{2}}\right)_{{n}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)_{{n}} \\ $$$$\left({x}\right)_{{m}\:{n}} ={m}^{{m}\:{n}} \underset{{k}=\mathrm{0}} {\overset{{m}=\mathrm{1}} {\prod}}\left(\frac{{x}+{k}}{{m}}\right)_{{n}} \:\:\:,\:{m}\in{z} \\ $$$${now}\:{if}\:{m}\:{is}\:{relative}\:{number}\:{such}\:{as}\frac{\mathrm{3}}{\mathrm{2}}\:,\:{m}\in{Q} \\ $$$$\left({x}\right)_{\frac{\mathrm{3}}{\mathrm{2}}{n}} =?? \\ $$$$ \\ $$$${help}\:{me}\: \\ $$
