Question Number 121996 by Anuragkar last updated on 13/Nov/20
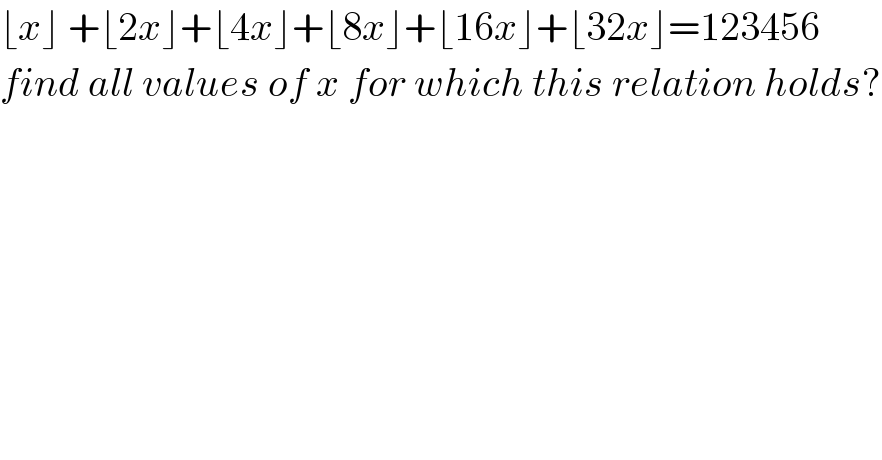
$$\lfloor{x}\rfloor\:+\lfloor\mathrm{2}{x}\rfloor+\lfloor\mathrm{4}{x}\rfloor+\lfloor\mathrm{8}{x}\rfloor+\lfloor\mathrm{16}{x}\rfloor+\lfloor\mathrm{32}{x}\rfloor=\mathrm{123456} \\ $$$${find}\:{all}\:{values}\:{of}\:{x}\:{for}\:{which}\:{this}\:{relation}\:{holds}? \\ $$
Answered by prakash jain last updated on 13/Nov/20
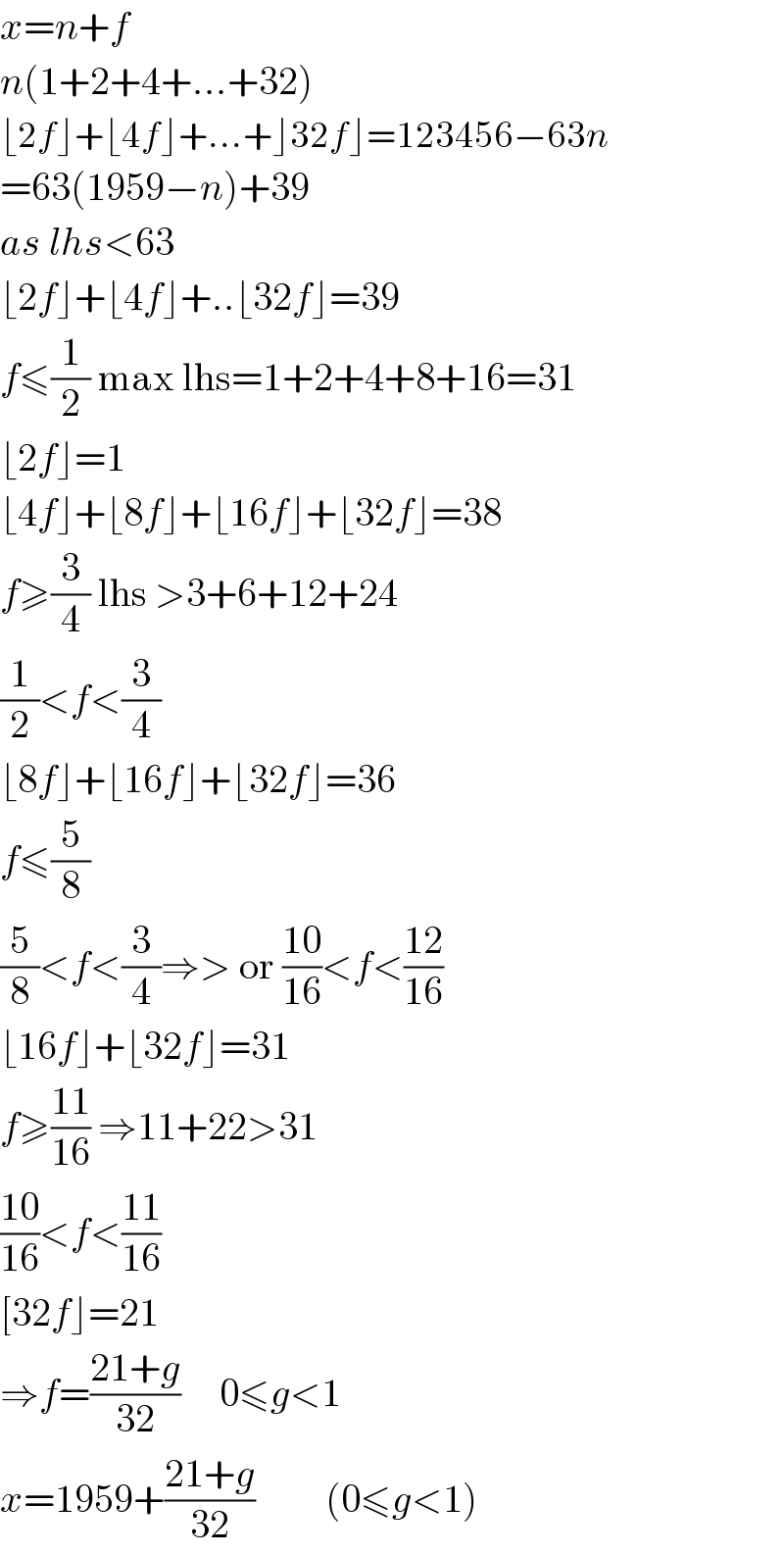
$${x}={n}+{f} \\ $$$${n}\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+…+\mathrm{32}\right) \\ $$$$\lfloor\mathrm{2}{f}\rfloor+\lfloor\mathrm{4}{f}\rfloor+…+\rfloor\mathrm{32}{f}\rfloor=\mathrm{123456}−\mathrm{63}{n} \\ $$$$=\mathrm{63}\left(\mathrm{1959}−{n}\right)+\mathrm{39} \\ $$$${as}\:{lhs}<\mathrm{63} \\ $$$$\lfloor\mathrm{2}{f}\rfloor+\lfloor\mathrm{4}{f}\rfloor+..\lfloor\mathrm{32}{f}\rfloor=\mathrm{39} \\ $$$${f}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{max}\:\mathrm{lhs}=\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{8}+\mathrm{16}=\mathrm{31} \\ $$$$\lfloor\mathrm{2}{f}\rfloor=\mathrm{1} \\ $$$$\lfloor\mathrm{4}{f}\rfloor+\lfloor\mathrm{8}{f}\rfloor+\lfloor\mathrm{16}{f}\rfloor+\lfloor\mathrm{32}{f}\rfloor=\mathrm{38} \\ $$$${f}\geqslant\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{lhs}\:>\mathrm{3}+\mathrm{6}+\mathrm{12}+\mathrm{24} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}<{f}<\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\lfloor\mathrm{8}{f}\rfloor+\lfloor\mathrm{16}{f}\rfloor+\lfloor\mathrm{32}{f}\rfloor=\mathrm{36} \\ $$$${f}\leqslant\frac{\mathrm{5}}{\mathrm{8}}\: \\ $$$$\frac{\mathrm{5}}{\mathrm{8}}<{f}<\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow>\:\mathrm{or}\:\frac{\mathrm{10}}{\mathrm{16}}<{f}<\frac{\mathrm{12}}{\mathrm{16}} \\ $$$$\lfloor\mathrm{16}{f}\rfloor+\lfloor\mathrm{32}{f}\rfloor=\mathrm{31} \\ $$$${f}\geqslant\frac{\mathrm{11}}{\mathrm{16}}\:\Rightarrow\mathrm{11}+\mathrm{22}>\mathrm{31} \\ $$$$\frac{\mathrm{10}}{\mathrm{16}}<{f}<\frac{\mathrm{11}}{\mathrm{16}} \\ $$$$\left[\mathrm{32}{f}\rfloor=\mathrm{21}\right. \\ $$$$\Rightarrow{f}=\frac{\mathrm{21}+{g}}{\mathrm{32}}\:\:\:\:\:\mathrm{0}\leqslant{g}<\mathrm{1} \\ $$$${x}=\mathrm{1959}+\frac{\mathrm{21}+{g}}{\mathrm{32}}\:\:\:\:\:\:\:\:\:\left(\mathrm{0}\leqslant{g}<\mathrm{1}\right) \\ $$
