Question Number 185076 by mathlove last updated on 16/Jan/23

$${x}^{\mathrm{2}{x}^{\mathrm{6}} } =\mathrm{3} \\ $$$${x}=? \\ $$
Answered by aba last updated on 16/Jan/23
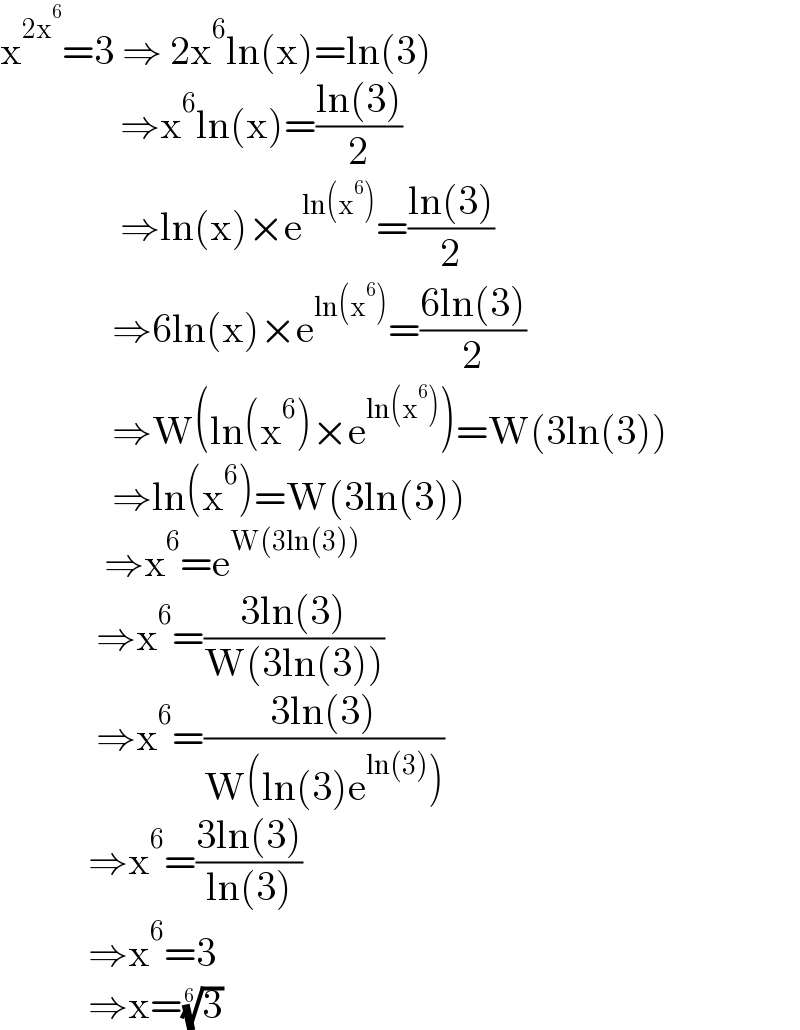
$$\mathrm{x}^{\mathrm{2x}^{\mathrm{6}} } =\mathrm{3}\:\Rightarrow\:\mathrm{2x}^{\mathrm{6}} \mathrm{ln}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} \mathrm{ln}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{ln}\left(\mathrm{x}\right)×\mathrm{e}^{\mathrm{ln}\left(\mathrm{x}^{\mathrm{6}} \right)} =\frac{\mathrm{ln}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{6ln}\left(\mathrm{x}\right)×\mathrm{e}^{\mathrm{ln}\left(\mathrm{x}^{\mathrm{6}} \right)} =\frac{\mathrm{6ln}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{W}\left(\mathrm{ln}\left(\mathrm{x}^{\mathrm{6}} \right)×\mathrm{e}^{\mathrm{ln}\left(\mathrm{x}^{\mathrm{6}} \right)} \right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{3}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{ln}\left(\mathrm{x}^{\mathrm{6}} \right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{3}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} =\mathrm{e}^{\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{3}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} =\frac{\mathrm{3ln}\left(\mathrm{3}\right)}{\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{3}\right)\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} =\frac{\mathrm{3ln}\left(\mathrm{3}\right)}{\mathrm{W}\left(\mathrm{ln}\left(\mathrm{3}\right)\mathrm{e}^{\mathrm{ln}\left(\mathrm{3}\right)} \right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} =\frac{\mathrm{3ln}\left(\mathrm{3}\right)}{\mathrm{ln}\left(\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}^{\mathrm{6}} =\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=\sqrt[{\mathrm{6}}]{\mathrm{3}} \\ $$
Answered by Frix last updated on 16/Jan/23
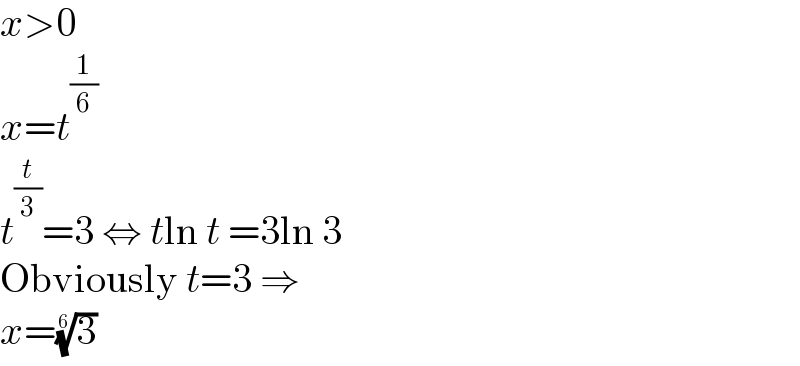
$${x}>\mathrm{0} \\ $$$${x}={t}^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$${t}^{\frac{{t}}{\mathrm{3}}} =\mathrm{3}\:\Leftrightarrow\:{t}\mathrm{ln}\:{t}\:=\mathrm{3ln}\:\mathrm{3} \\ $$$$\mathrm{Obviously}\:{t}=\mathrm{3}\:\Rightarrow \\ $$$${x}=\sqrt[{\mathrm{6}}]{\mathrm{3}} \\ $$
