Question Number 91491 by jagoll last updated on 01/May/20
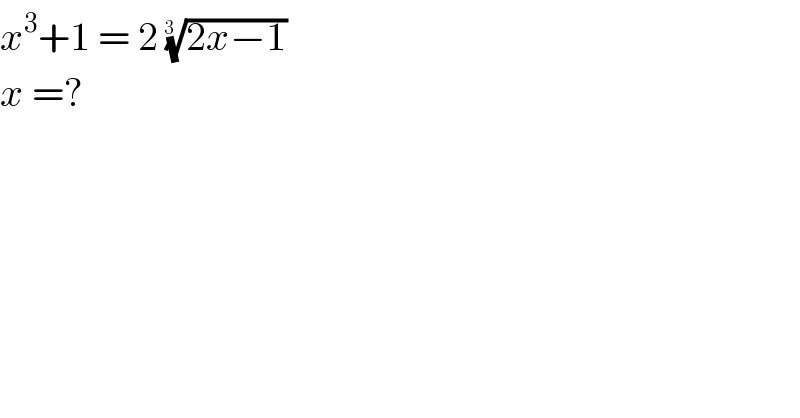
$${x}^{\mathrm{3}} +\mathrm{1}\:=\:\mathrm{2}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}{x}−\mathrm{1}} \\ $$$${x}\:=? \\ $$
Answered by MJS last updated on 01/May/20

$$\mathrm{obviously}\:{x}=\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}} =\mathrm{8}\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$${x}^{\mathrm{9}} +\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{16}{x}+\mathrm{9}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{8}} +{x}^{\mathrm{7}} +{x}^{\mathrm{6}} +\mathrm{4}{x}^{\mathrm{5}} +\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{approximately}\:\mathrm{solving}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}\approx−\mathrm{1}.\mathrm{61803}\vee{x}\approx.\mathrm{618034} \\ $$$$\mathrm{these}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{yes}! \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\left({x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{use}\:\mathrm{approximation}\:\mathrm{by}\:\mathrm{an} \\ $$$$\mathrm{electronic}\:\mathrm{calculator} \\ $$$${x}\approx−\mathrm{1}.\mathrm{08891}\pm.\mathrm{824866i} \\ $$$${x}\approx.\mathrm{123133}\pm\mathrm{1}.\mathrm{43020i} \\ $$$${x}\approx.\mathrm{965776}\pm\mathrm{1}.\mathrm{18647i} \\ $$$$\mathrm{only}\:\mathrm{these}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}: \\ $$$${x}=\mathrm{1} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}\approx−\mathrm{1}.\mathrm{08891}\pm.\mathrm{824866i} \\ $$
Commented by jagoll last updated on 01/May/20
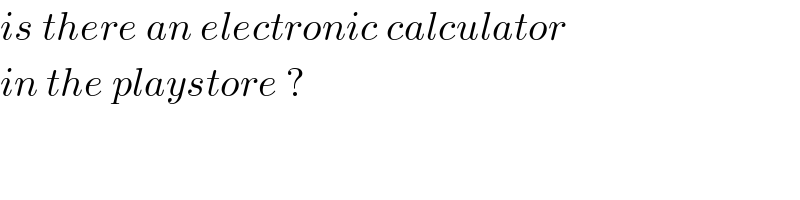
$${is}\:{there}\:{an}\:{electronic}\:{calculator} \\ $$$${in}\:{the}\:{playstore}\:? \\ $$
Commented by MJS last updated on 01/May/20
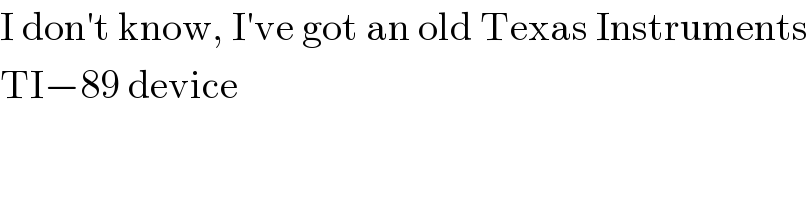
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know},\:\mathrm{I}'\mathrm{ve}\:\mathrm{got}\:\mathrm{an}\:\mathrm{old}\:\mathrm{Texas}\:\mathrm{Instruments} \\ $$$$\mathrm{TI}−\mathrm{89}\:\mathrm{device} \\ $$
Commented by jagoll last updated on 01/May/20

$${thank}\:{a}\:{lot}\:{sir} \\ $$
