Question Number 153152 by puissant last updated on 05/Sep/21
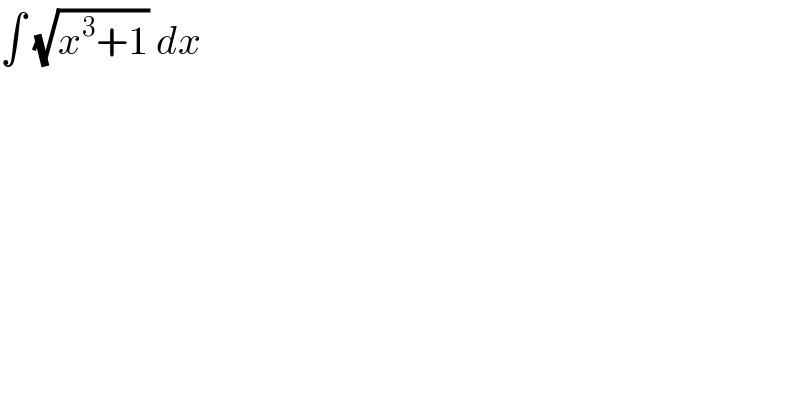
$$\int\:\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx} \\ $$
Answered by peter frank last updated on 05/Sep/21
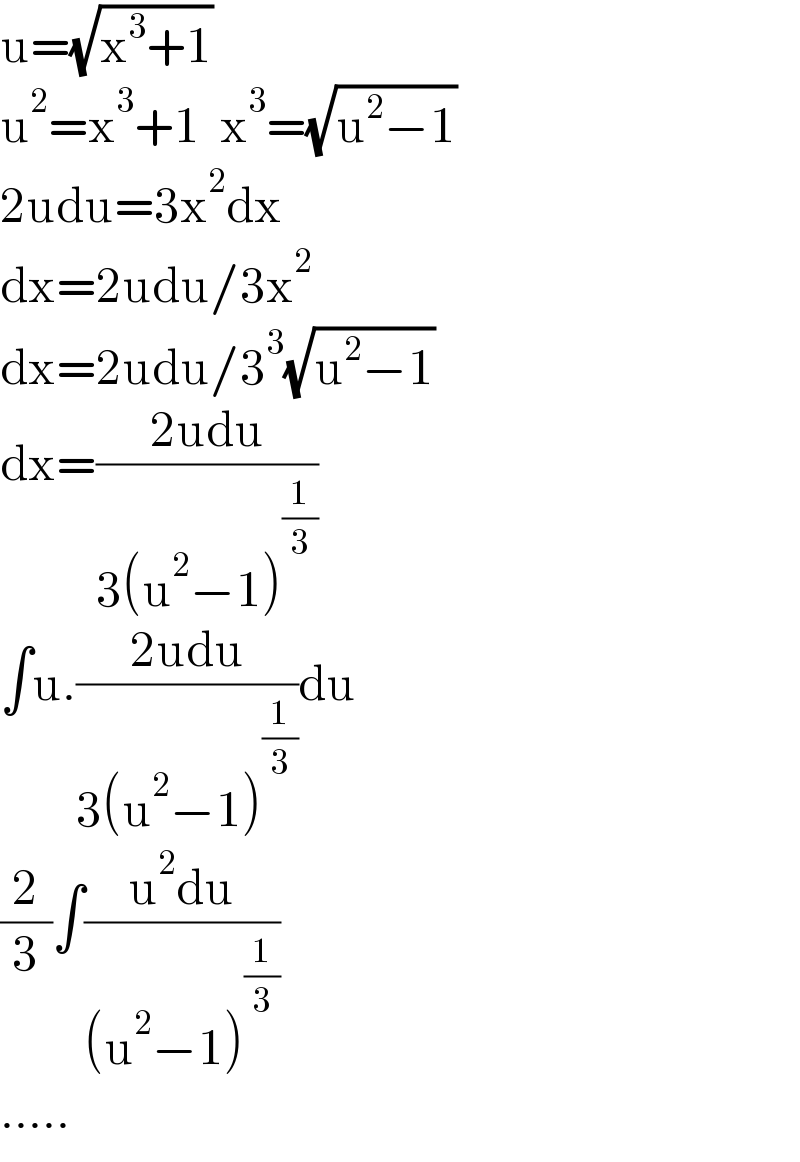
$$\mathrm{u}=\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$\mathrm{u}^{\mathrm{2}} =\mathrm{x}^{\mathrm{3}} +\mathrm{1}\:\:\mathrm{x}^{\mathrm{3}} =\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{2udu}=\mathrm{3x}^{\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{dx}=\mathrm{2udu}/\mathrm{3x}^{\mathrm{2}} \\ $$$$\mathrm{dx}=\mathrm{2udu}/\mathrm{3}^{\mathrm{3}} \sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{dx}=\frac{\mathrm{2udu}}{\mathrm{3}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\int\mathrm{u}.\frac{\mathrm{2udu}}{\mathrm{3}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }\mathrm{du} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{u}^{\mathrm{2}} \mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$….. \\ $$
Commented by peter frank last updated on 05/Sep/21
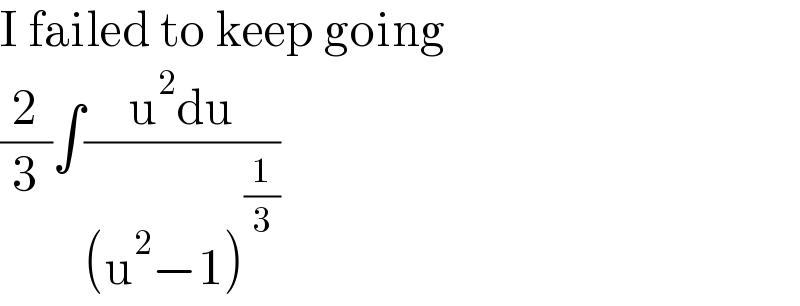
$$\mathrm{I}\:\mathrm{failed}\:\mathrm{to}\:\mathrm{keep}\:\mathrm{going} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{u}^{\mathrm{2}} \mathrm{du}}{\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$
Answered by aleks041103 last updated on 05/Sep/21

$${This}\:{integral}\:{doesn}'{t}\:{have}\:{solution} \\ $$$${in}\:{elementary}\:{functions}. \\ $$
