Question Number 93144 by i jagooll last updated on 11/May/20
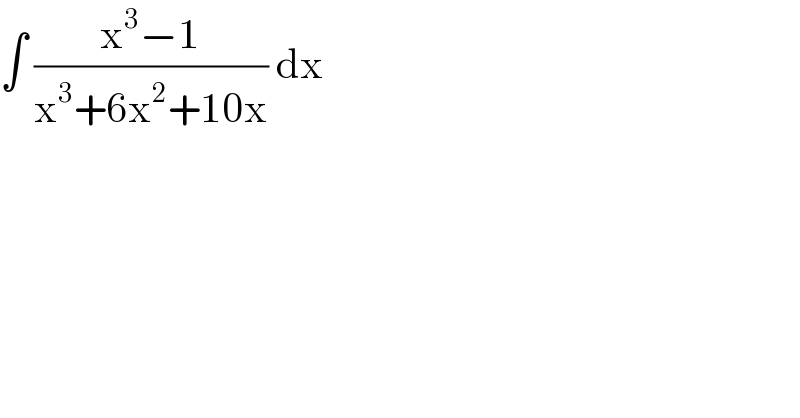
$$\int\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{10x}}\:\mathrm{dx}\: \\ $$
Answered by MJS last updated on 11/May/20
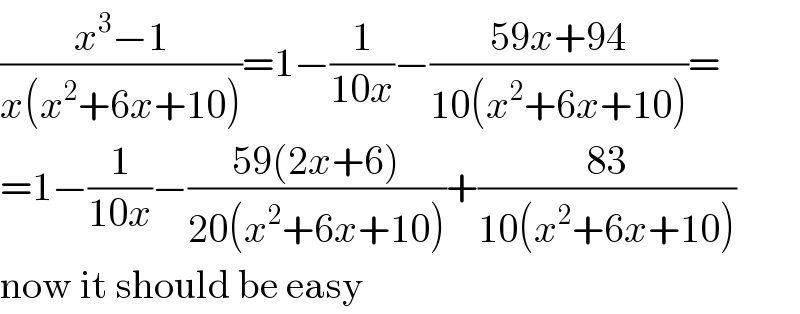
$$\frac{{x}^{\mathrm{3}} −\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}\right)}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}{x}}−\frac{\mathrm{59}{x}+\mathrm{94}}{\mathrm{10}\left({x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}\right)}= \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}{x}}−\frac{\mathrm{59}\left(\mathrm{2}{x}+\mathrm{6}\right)}{\mathrm{20}\left({x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}\right)}+\frac{\mathrm{83}}{\mathrm{10}\left({x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{10}\right)} \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy} \\ $$
Commented by i jagooll last updated on 11/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by MJS last updated on 11/May/20

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Commented by john santu last updated on 11/May/20
waw math lover sir
