Menu Close

x-3-2-1-solve-for-real-x-

Tinku Tara 0 Comments
Pin




Question Number 81519 by ajfour last updated on 13/Feb/20
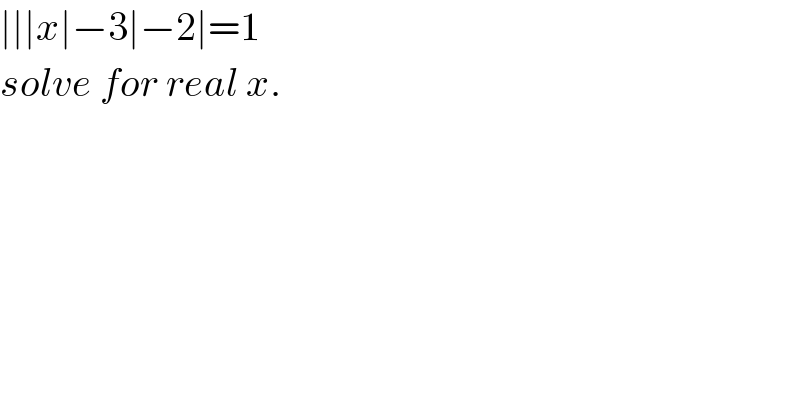
∣∣∣x∣−3∣−2∣=1 solve for real x.
$$\mid\mid\mid{x}\mid−\mathrm{3}\mid−\mathrm{2}\mid=\mathrm{1} \\ $$$${solve}\:{for}\:{real}\:{x}. \\ $$
Commented by mr W last updated on 13/Feb/20
∣∣∣x∣−3∣−2∣=1 ∣∣x∣−3∣−2=±1 ∣∣x∣−3∣=2±1 ∣x∣−3=±(2±1) ∣x∣=3±(2±1) ⇒x=±[3±(2±1)]=0,±2, ±4, ±6
$$\mid\mid\mid{x}\mid−\mathrm{3}\mid−\mathrm{2}\mid=\mathrm{1} \\ $$$$\mid\mid{x}\mid−\mathrm{3}\mid−\mathrm{2}=\pm\mathrm{1} \\ $$$$\mid\mid{x}\mid−\mathrm{3}\mid=\mathrm{2}\pm\mathrm{1} \\ $$$$\mid{x}\mid−\mathrm{3}=\pm\left(\mathrm{2}\pm\mathrm{1}\right) \\ $$$$\mid{x}\mid=\mathrm{3}\pm\left(\mathrm{2}\pm\mathrm{1}\right) \\ $$$$\Rightarrow{x}=\pm\left[\mathrm{3}\pm\left(\mathrm{2}\pm\mathrm{1}\right)\right]=\mathrm{0},\pm\mathrm{2},\:\pm\mathrm{4},\:\pm\mathrm{6} \\ $$
Commented by ajfour last updated on 13/Feb/20
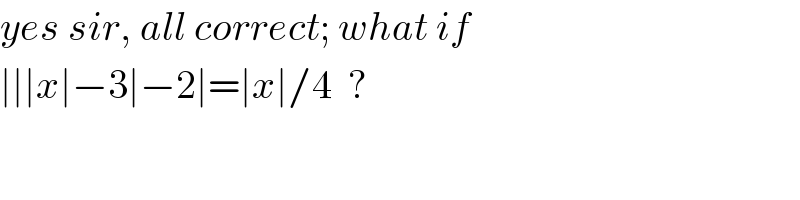
yes sir, all correct; what if ∣∣∣x∣−3∣−2∣=∣x∣/4 ?
$${yes}\:{sir},\:{all}\:{correct};\:{what}\:{if} \\ $$$$\mid\mid\mid{x}\mid−\mathrm{3}\mid−\mathrm{2}\mid=\mid{x}\mid/\mathrm{4}\:\:? \\ $$
Commented by mr W last updated on 13/Feb/20
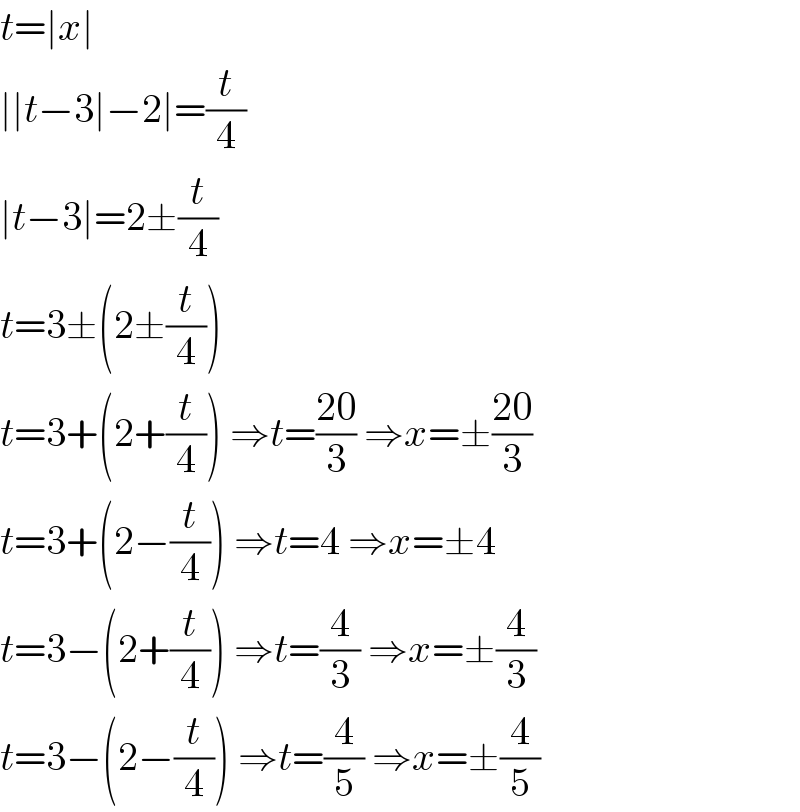
t=∣x∣ ∣∣t−3∣−2∣=(t/4) ∣t−3∣=2±(t/4) t=3±(2±(t/4)) t=3+(2+(t/4)) ⇒t=((20)/3) ⇒x=±((20)/3) t=3+(2−(t/4)) ⇒t=4 ⇒x=±4 t=3−(2+(t/4)) ⇒t=(4/3) ⇒x=±(4/3) t=3−(2−(t/4)) ⇒t=(4/5) ⇒x=±(4/5)
$${t}=\mid{x}\mid \\ $$$$\mid\mid{t}−\mathrm{3}\mid−\mathrm{2}\mid=\frac{{t}}{\mathrm{4}} \\ $$$$\mid{t}−\mathrm{3}\mid=\mathrm{2}\pm\frac{{t}}{\mathrm{4}} \\ $$$${t}=\mathrm{3}\pm\left(\mathrm{2}\pm\frac{{t}}{\mathrm{4}}\right) \\ $$$${t}=\mathrm{3}+\left(\mathrm{2}+\frac{{t}}{\mathrm{4}}\right)\:\Rightarrow{t}=\frac{\mathrm{20}}{\mathrm{3}}\:\Rightarrow{x}=\pm\frac{\mathrm{20}}{\mathrm{3}} \\ $$$${t}=\mathrm{3}+\left(\mathrm{2}−\frac{{t}}{\mathrm{4}}\right)\:\Rightarrow{t}=\mathrm{4}\:\Rightarrow{x}=\pm\mathrm{4} \\ $$$${t}=\mathrm{3}−\left(\mathrm{2}+\frac{{t}}{\mathrm{4}}\right)\:\Rightarrow{t}=\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow{x}=\pm\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${t}=\mathrm{3}−\left(\mathrm{2}−\frac{{t}}{\mathrm{4}}\right)\:\Rightarrow{t}=\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow{x}=\pm\frac{\mathrm{4}}{\mathrm{5}} \\ $$
Commented by ajfour last updated on 13/Feb/20
Wonderful, Sir, very beautiful!
$${Wonderful},\:{Sir},\:{very}\:{beautiful}! \\ $$
Answered by behi83417@gmail.com last updated on 13/Feb/20
x=±2,±4
$$\mathrm{x}=\pm\mathrm{2},\pm\mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *