Question Number 89226 by cindiaulia last updated on 16/Apr/20
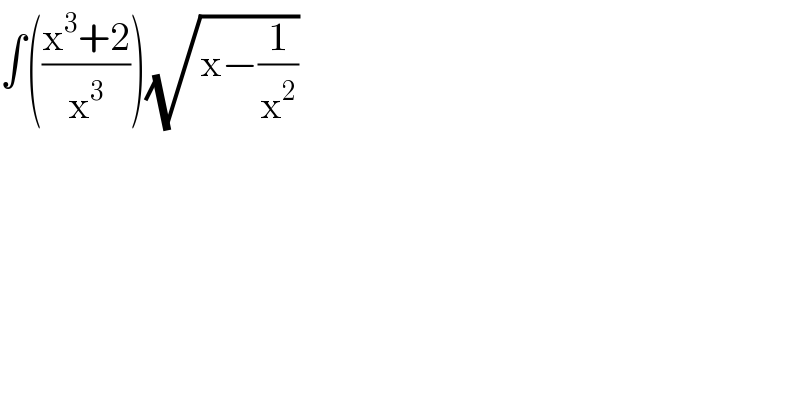
$$\int\left(\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\right)\sqrt{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$
Commented by jagoll last updated on 16/Apr/20
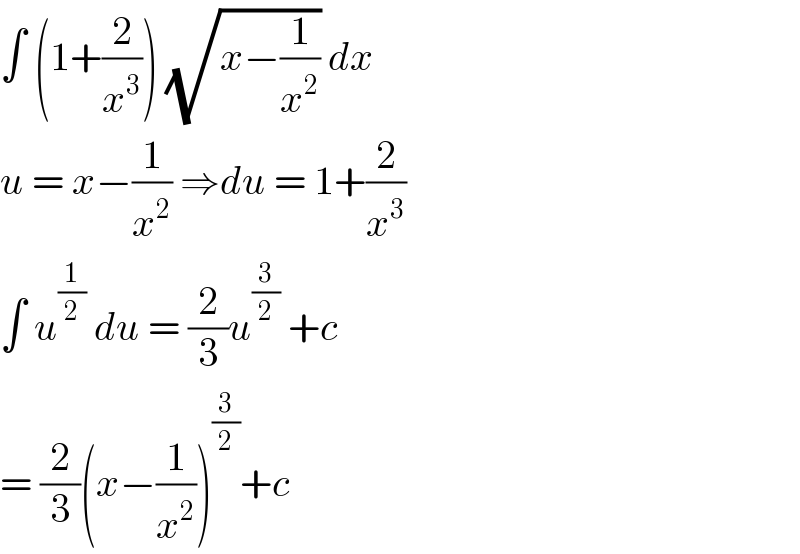
$$\int\:\left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\right)\:\sqrt{{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx}\: \\ $$$${u}\:=\:{x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\Rightarrow{du}\:=\:\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{3}} } \\ $$$$\int\:{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \:{du}\:=\:\frac{\mathrm{2}}{\mathrm{3}}{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+{c} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\left({x}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{c} \\ $$
