Question Number 149041 by mathdanisur last updated on 02/Aug/21
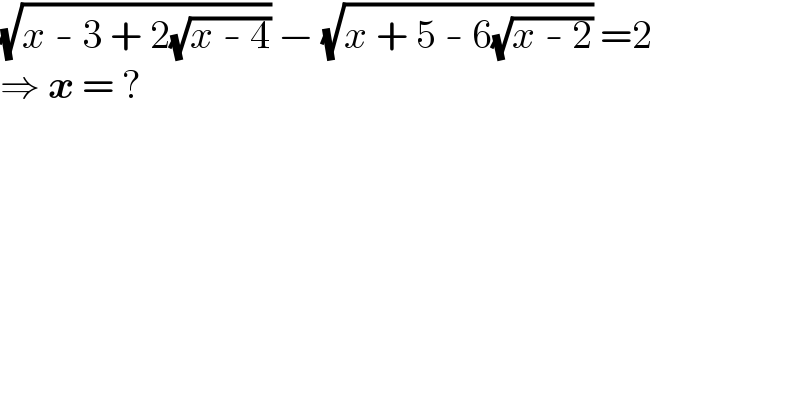
$$\sqrt{{x}\:-\:\mathrm{3}\:+\:\mathrm{2}\sqrt{{x}\:-\:\mathrm{4}}}\:−\:\sqrt{{x}\:+\:\mathrm{5}\:-\:\mathrm{6}\sqrt{{x}\:-\:\mathrm{2}}}\:=\mathrm{2} \\ $$$$\Rightarrow\:\boldsymbol{{x}}\:=\:? \\ $$
Commented by bramlexs22 last updated on 02/Aug/21

Commented by MJS_new last updated on 02/Aug/21
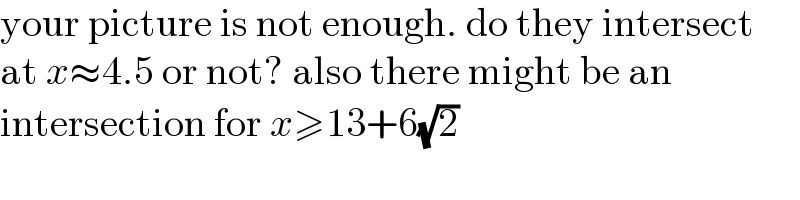
$$\mathrm{your}\:\mathrm{picture}\:\mathrm{is}\:\mathrm{not}\:\mathrm{enough}.\:\mathrm{do}\:\mathrm{they}\:\mathrm{intersect} \\ $$$$\mathrm{at}\:{x}\approx\mathrm{4}.\mathrm{5}\:\mathrm{or}\:\mathrm{not}?\:\mathrm{also}\:\mathrm{there}\:\mathrm{might}\:\mathrm{be}\:\mathrm{an} \\ $$$$\mathrm{intersection}\:\mathrm{for}\:{x}\geqslant\mathrm{13}+\mathrm{6}\sqrt{\mathrm{2}} \\ $$
Commented by bramlexs22 last updated on 02/Aug/21
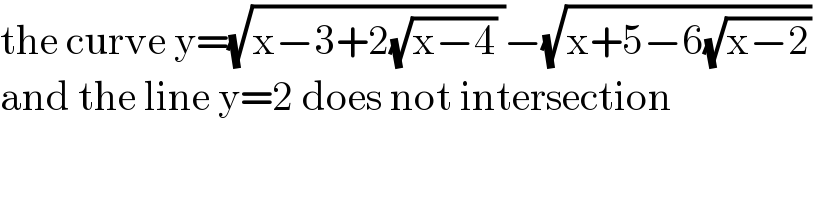
$$\mathrm{the}\:\mathrm{curve}\:\mathrm{y}=\sqrt{\mathrm{x}−\mathrm{3}+\mathrm{2}\sqrt{\mathrm{x}−\mathrm{4}}\:}−\sqrt{\mathrm{x}+\mathrm{5}−\mathrm{6}\sqrt{\mathrm{x}−\mathrm{2}}}\: \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2}\:\mathrm{does}\:\mathrm{not}\:\mathrm{intersection} \\ $$
Answered by MJS_new last updated on 02/Aug/21

$${f}_{\mathrm{1}} \left({x}\right)=\sqrt{{x}−\mathrm{3}+\mathrm{2}\sqrt{{x}−\mathrm{4}}} \\ $$$$\:\:\:\:\:\mathrm{defined}\:\mathrm{for}\:{x}\geqslant\mathrm{4} \\ $$$$\:\:\:\:\:\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{for}\:{x}\geqslant\mathrm{4} \\ $$$${f}_{\mathrm{2}} \left({x}\right)=\sqrt{{x}+\mathrm{5}−\mathrm{6}\sqrt{{x}−\mathrm{2}}} \\ $$$$\:\:\:\:\:\mathrm{defined}\:\mathrm{for}\:\mathrm{2}\leqslant{x}\leqslant\mathrm{13}−\mathrm{6}\sqrt{\mathrm{2}}\:\vee\:{x}\geqslant\mathrm{13}+\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{strictly}\:\mathrm{decreasing}\:\mathrm{for}\:\mathrm{2}\leqslant{x}\leqslant\mathrm{13}−\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{for}\:{x}\geqslant\mathrm{13}+\mathrm{6}\sqrt{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{4}\leqslant{x}\leqslant\mathrm{13}−\mathrm{6}\sqrt{\mathrm{2}}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{of} \\ $$$${f}_{\mathrm{1}} \left({x}\right)−{f}_{\mathrm{2}} \left({x}\right)=\sqrt{\mathrm{10}−\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{6}}}\approx\mathrm{1}.\mathrm{72}<\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{for}\:{x}\geqslant\mathrm{13}+\mathrm{2}\sqrt{\mathrm{6}}:\:\mathrm{4}<{f}_{\mathrm{1}} \left({x}\right)−{f}_{\mathrm{2}} \left({x}\right)\leqslant\sqrt{\mathrm{10}+\mathrm{6}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{6}}}\approx\mathrm{5}.\mathrm{18} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$
