Question Number 13360 by tawa tawa last updated on 19/May/17
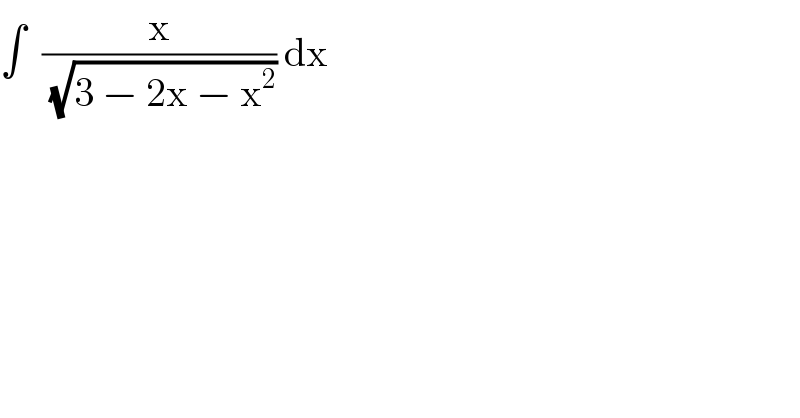
$$\int\:\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{3}\:−\:\mathrm{2x}\:−\:\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 19/May/17
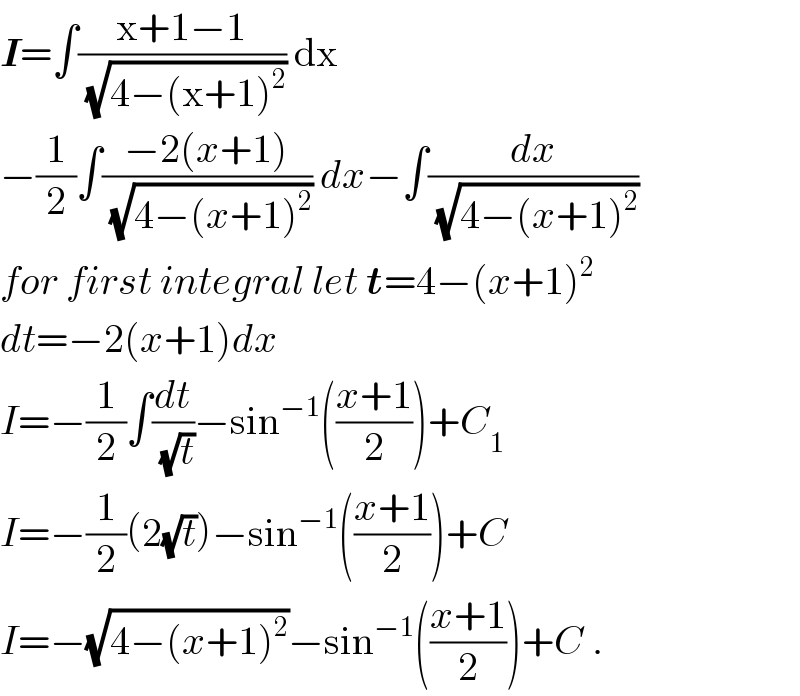
$$\boldsymbol{{I}}=\int\frac{\mathrm{x}+\mathrm{1}−\mathrm{1}}{\:\sqrt{\mathrm{4}−\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:\mathrm{dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}\left({x}+\mathrm{1}\right)}{\:\sqrt{\mathrm{4}−\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}\:{dx}−\int\frac{{dx}}{\:\sqrt{\mathrm{4}−\left({x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$${for}\:{first}\:{integral}\:{let}\:\boldsymbol{{t}}=\mathrm{4}−\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${dt}=−\mathrm{2}\left({x}+\mathrm{1}\right){dx} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\:\sqrt{{t}}}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+{C}_{\mathrm{1}} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{{t}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+{C} \\ $$$${I}=−\sqrt{\mathrm{4}−\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)+{C}\:. \\ $$
Commented by tawa tawa last updated on 19/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
