x-3-3-4-dx-

Question Number 120943 by Jamshidbek2311 last updated on 04/Nov/20

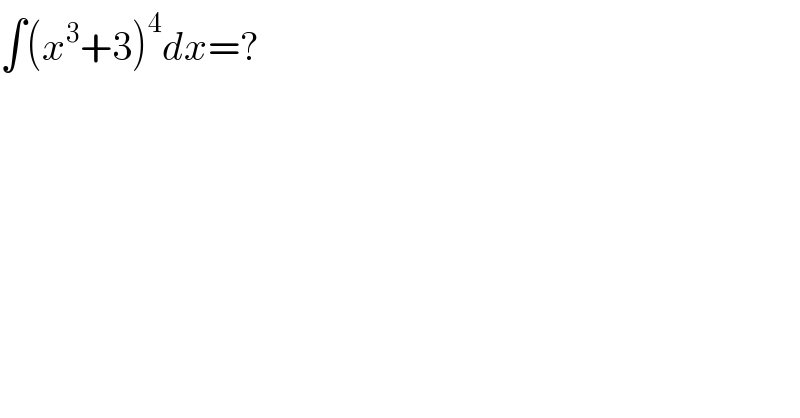
$$\int\left({x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{4}} {dx}=? \\ $$

Commented by mathmax by abdo last updated on 05/Nov/20

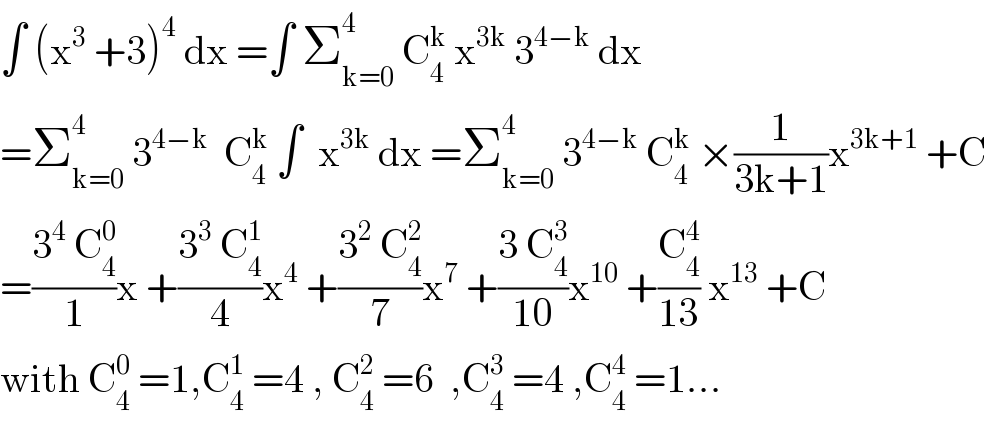
∫ (x^3 +3)^4 dx =∫ Σ_(k=0) ^4 C_4 ^k x^(3k) 3^(4−k) dx =Σ_(k=0) ^4 3^(4−k) C_4 ^k ∫ x^(3k) dx =Σ_(k=0) ^4 3^(4−k) C_4 ^k ×(1/(3k+1))x^(3k+1) +C =((3^4 C_4 ^0 )/1)x +((3^3 C_4 ^1 )/4)x^4 +((3^2 C_4 ^2 )/7)x^7 +((3 C_4 ^3 )/(10))x^(10) +(C_4 ^4 /(13)) x^(13) +C with C_4 ^0 =1,C_4 ^1 =4 , C_4 ^2 =6 ,C_4 ^3 =4 ,C_4 ^4 =1...

$$\int\:\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{3}\right)^{\mathrm{4}} \:\mathrm{dx}\:=\int\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{3k}} \:\mathrm{3}^{\mathrm{4}−\mathrm{k}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{3}^{\mathrm{4}−\mathrm{k}} \:\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\int\:\:\mathrm{x}^{\mathrm{3k}} \:\mathrm{dx}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{3}^{\mathrm{4}−\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:×\frac{\mathrm{1}}{\mathrm{3k}+\mathrm{1}}\mathrm{x}^{\mathrm{3k}+\mathrm{1}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{3}^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{0}} }{\mathrm{1}}\mathrm{x}\:+\frac{\mathrm{3}^{\mathrm{3}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} }{\mathrm{4}}\mathrm{x}^{\mathrm{4}} \:+\frac{\mathrm{3}^{\mathrm{2}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{2}} }{\mathrm{7}}\mathrm{x}^{\mathrm{7}} \:+\frac{\mathrm{3}\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{3}} }{\mathrm{10}}\mathrm{x}^{\mathrm{10}} \:+\frac{\mathrm{C}_{\mathrm{4}} ^{\mathrm{4}} }{\mathrm{13}}\:\mathrm{x}^{\mathrm{13}} \:+\mathrm{C} \\ $$$$\mathrm{with}\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{0}} \:=\mathrm{1},\mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} \:=\mathrm{4}\:,\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{2}} \:=\mathrm{6}\:\:,\mathrm{C}_{\mathrm{4}} ^{\mathrm{3}} \:=\mathrm{4}\:,\mathrm{C}_{\mathrm{4}} ^{\mathrm{4}} \:=\mathrm{1}… \\ $$

Answered by 675480065 last updated on 04/Nov/20

$$\frac{\left({x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{5}} }{\mathrm{5}\left(\mathrm{3}{x}^{\mathrm{2}} \right)}+{k} \\ $$

Commented by MJS_new last updated on 04/Nov/20

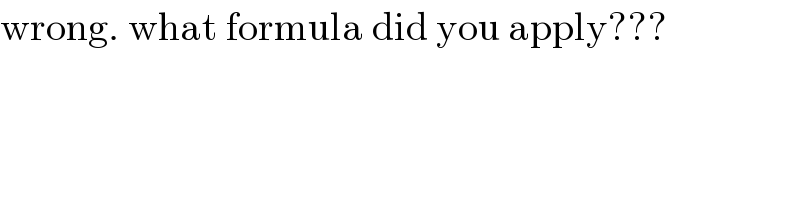
$$\mathrm{wrong}.\:\mathrm{what}\:\mathrm{formula}\:\mathrm{did}\:\mathrm{you}\:\mathrm{apply}??? \\ $$

Commented by mathmax by abdo last updated on 04/Nov/20

$$\mathrm{not}\:\mathrm{correct}\:…! \\ $$

Answered by Olaf last updated on 04/Nov/20

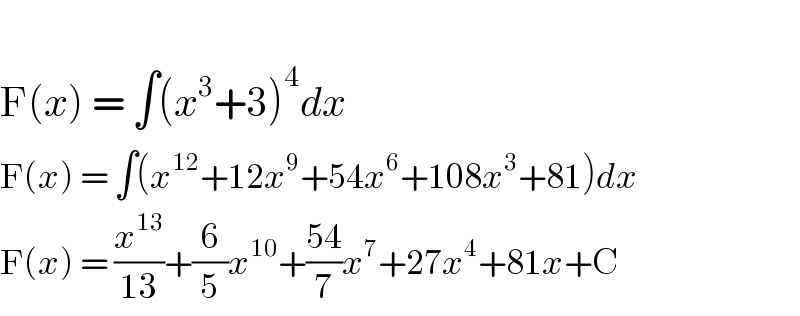
F(x) = ∫(x^3 +3)^4 dx F(x) = ∫(x^(12) +12x^9 +54x^6 +108x^3 +81)dx F(x) = (x^(13) /(13))+(6/5)x^(10) +((54)/7)x^7 +27x^4 +81x+C

$$ \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\left({x}^{\mathrm{3}} +\mathrm{3}\right)^{\mathrm{4}} {dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\left({x}^{\mathrm{12}} +\mathrm{12}{x}^{\mathrm{9}} +\mathrm{54}{x}^{\mathrm{6}} +\mathrm{108}{x}^{\mathrm{3}} +\mathrm{81}\right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{{x}^{\mathrm{13}} }{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{5}}{x}^{\mathrm{10}} +\frac{\mathrm{54}}{\mathrm{7}}{x}^{\mathrm{7}} +\mathrm{27}{x}^{\mathrm{4}} +\mathrm{81}{x}+\mathrm{C} \\ $$

Answered by Dwaipayan Shikari last updated on 04/Nov/20

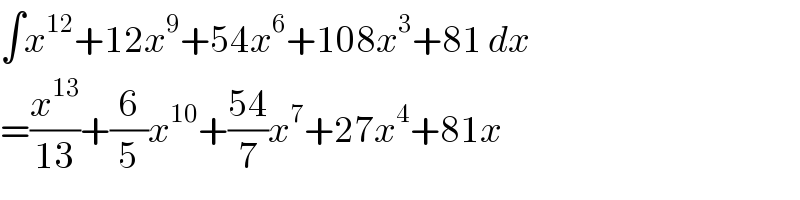
∫x^(12) +12x^9 +54x^6 +108x^3 +81 dx =(x^(13) /(13))+(6/5)x^(10) +((54)/7)x^7 +27x^4 +81x

$$\int{x}^{\mathrm{12}} +\mathrm{12}{x}^{\mathrm{9}} +\mathrm{54}{x}^{\mathrm{6}} +\mathrm{108}{x}^{\mathrm{3}} +\mathrm{81}\:{dx} \\ $$$$=\frac{{x}^{\mathrm{13}} }{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{5}}{x}^{\mathrm{10}} +\frac{\mathrm{54}}{\mathrm{7}}{x}^{\mathrm{7}} +\mathrm{27}{x}^{\mathrm{4}} +\mathrm{81}{x} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply