Question Number 151403 by 7770 last updated on 20/Aug/21

Commented by mr W last updated on 20/Aug/21

Commented by 7770 last updated on 20/Aug/21
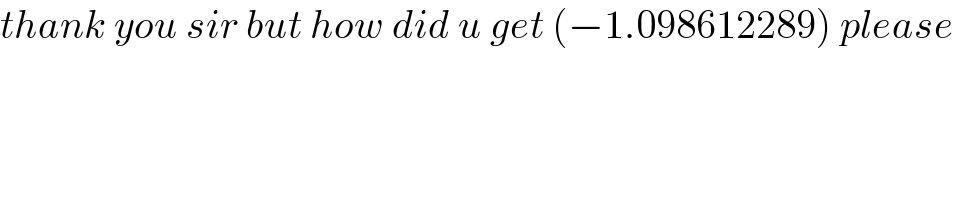
Commented by mr W last updated on 21/Aug/21

Commented by 7770 last updated on 21/Aug/21

Commented by otchereabdullai@gmail.com last updated on 22/Aug/21

