Question Number 150752 by Jamshidbek last updated on 15/Aug/21

$$\mathrm{x}^{\mathrm{3}} +\mathrm{3x}+\mathrm{12}=\mathrm{0}\:\:\mathrm{solve}\:\mathrm{real}\:\mathrm{number}\: \\ $$$$\mathrm{help} \\ $$
Commented by liberty last updated on 15/Aug/21
x = root(3, - root(2, 37) - 6) - (1/root(3, - root(2, 37) - 6))
Commented by liberty last updated on 15/Aug/21

Answered by mr W last updated on 15/Aug/21
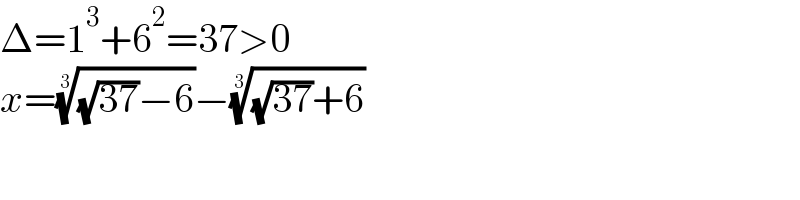
$$\Delta=\mathrm{1}^{\mathrm{3}} +\mathrm{6}^{\mathrm{2}} =\mathrm{37}>\mathrm{0} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{37}}−\mathrm{6}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{37}}+\mathrm{6}} \\ $$
Commented by puissant last updated on 15/Aug/21

$${sir}\:{it}\:{is}\:{the}\:{formula}\:{of}\:{Tartaglia}..? \\ $$
Commented by mr W last updated on 15/Aug/21

$${cardano}'{s} \\ $$
Commented by puissant last updated on 15/Aug/21

$$\Rightarrow\:{x}^{\mathrm{3}} =−\mathrm{3}{x}−\mathrm{12} \\ $$$${x}=\sqrt[{\mathrm{3}}]{−\mathrm{6}+\sqrt{\mathrm{37}}}−\sqrt[{\mathrm{3}}]{\mathrm{6}+\sqrt{\mathrm{37}}}\:\:{sorry}\:{sir}.. \\ $$
Commented by naka3546 last updated on 15/Aug/21

$${may}\:\:{be}\:\:: \\ $$$${x}\:\:=\:\:\frac{\sqrt[{\mathrm{3}}]{\left(\sqrt{\mathrm{37}}\:−\:\mathrm{6}\right)^{\mathrm{2}} }−\:\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{37}}\:−\:\mathrm{6}}} \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{37}}\:−\:\mathrm{6}}\:\:−\:\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{37}}\:+\:\mathrm{6}} \\ $$
Commented by Tawa11 last updated on 15/Aug/21

