Menu Close

x-3-4-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 85648 by sakeefhasan05@gmail.com last updated on 23/Mar/20
∫(((x^3 −4))/((x+1)))dx
$$\int\frac{\left(\mathrm{x}^{\mathrm{3}} −\mathrm{4}\right)}{\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$
Answered by petrochengula last updated on 23/Mar/20
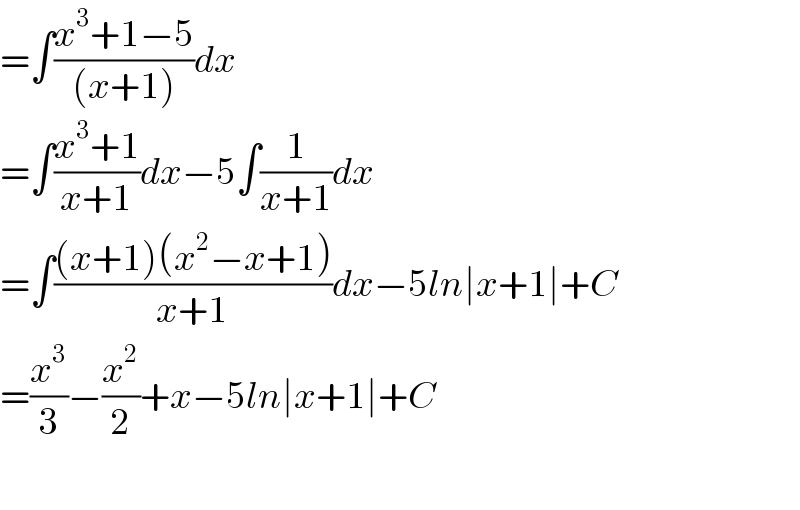
=∫((x^3 +1−5)/((x+1)))dx =∫((x^3 +1)/(x+1))dx−5∫(1/(x+1))dx =∫(((x+1)(x^2 −x+1))/(x+1))dx−5ln∣x+1∣+C =(x^3 /3)−(x^2 /2)+x−5ln∣x+1∣+C
$$=\int\frac{{x}^{\mathrm{3}} +\mathrm{1}−\mathrm{5}}{\left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}+\mathrm{1}}{dx}−\mathrm{5}\int\frac{\mathrm{1}}{{x}+\mathrm{1}}{dx} \\ $$$$=\int\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}+\mathrm{1}}{dx}−\mathrm{5}{ln}\mid{x}+\mathrm{1}\mid+{C} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}−\mathrm{5}{ln}\mid{x}+\mathrm{1}\mid+{C} \\ $$$$ \\ $$
Answered by petrochengula last updated on 23/Mar/20
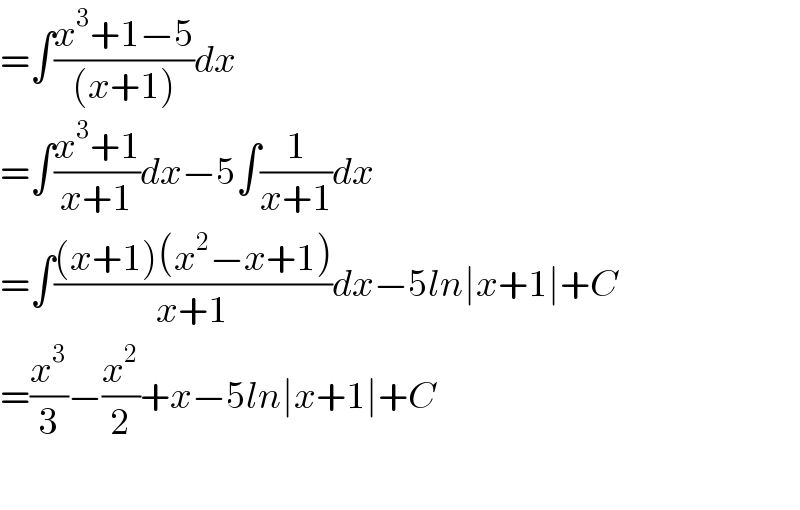
=∫((x^3 +1−5)/((x+1)))dx =∫((x^3 +1)/(x+1))dx−5∫(1/(x+1))dx =∫(((x+1)(x^2 −x+1))/(x+1))dx−5ln∣x+1∣+C =(x^3 /3)−(x^2 /2)+x−5ln∣x+1∣+C
$$=\int\frac{{x}^{\mathrm{3}} +\mathrm{1}−\mathrm{5}}{\left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\int\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}+\mathrm{1}}{dx}−\mathrm{5}\int\frac{\mathrm{1}}{{x}+\mathrm{1}}{dx} \\ $$$$=\int\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}+\mathrm{1}}{dx}−\mathrm{5}{ln}\mid{x}+\mathrm{1}\mid+{C} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}−\mathrm{5}{ln}\mid{x}+\mathrm{1}\mid+{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *