Question Number 156921 by cortano last updated on 17/Oct/21
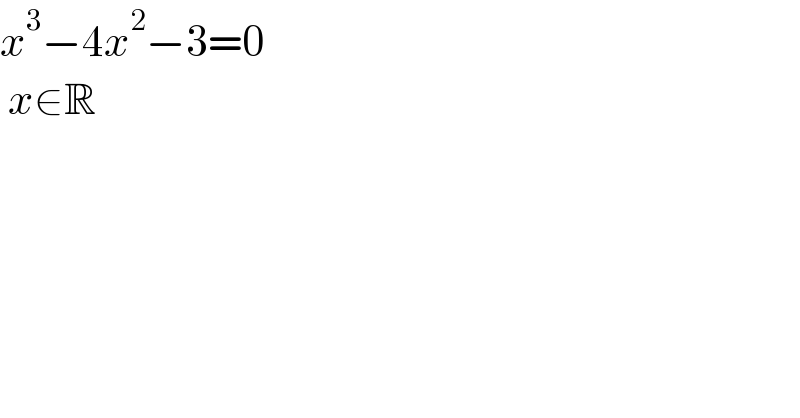
$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$$\:{x}\in\mathbb{R} \\ $$
Answered by mr W last updated on 17/Oct/21
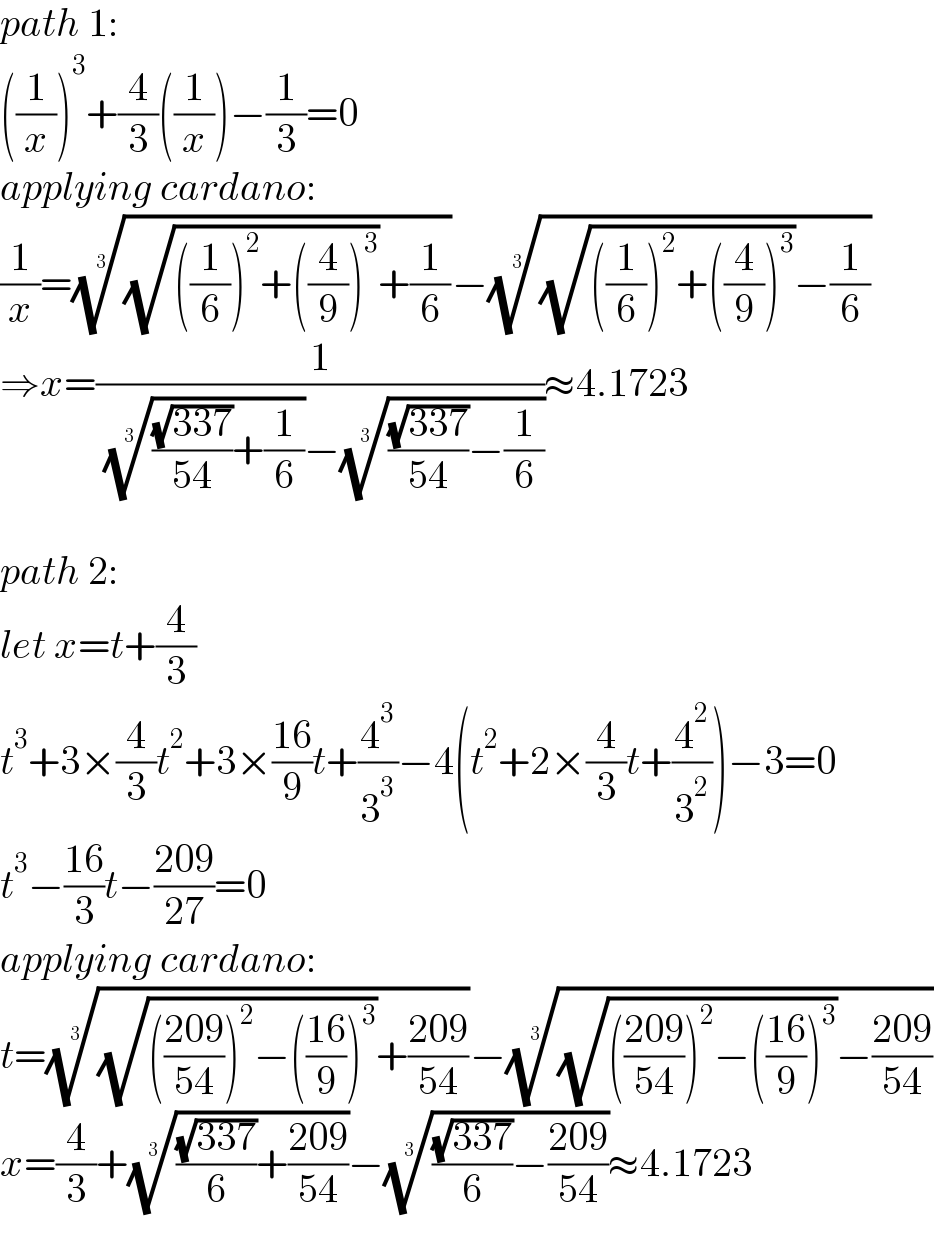
$${path}\:\mathrm{1}: \\ $$$$\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} +\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$${applying}\:{cardano}: \\ $$$$\frac{\mathrm{1}}{{x}}=\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{6}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{337}}}{\mathrm{54}}+\frac{\mathrm{1}}{\mathrm{6}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{337}}}{\mathrm{54}}−\frac{\mathrm{1}}{\mathrm{6}}}}\approx\mathrm{4}.\mathrm{1723} \\ $$$$ \\ $$$${path}\:\mathrm{2}: \\ $$$${let}\:{x}={t}+\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} +\mathrm{3}×\frac{\mathrm{4}}{\mathrm{3}}{t}^{\mathrm{2}} +\mathrm{3}×\frac{\mathrm{16}}{\mathrm{9}}{t}+\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }−\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{4}}{\mathrm{3}}{t}+\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }\right)−\mathrm{3}=\mathrm{0} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{16}}{\mathrm{3}}{t}−\frac{\mathrm{209}}{\mathrm{27}}=\mathrm{0} \\ $$$${applying}\:{cardano}: \\ $$$${t}=\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{209}}{\mathrm{54}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{16}}{\mathrm{9}}\right)^{\mathrm{3}} }+\frac{\mathrm{209}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\sqrt{\left(\frac{\mathrm{209}}{\mathrm{54}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{16}}{\mathrm{9}}\right)^{\mathrm{3}} }−\frac{\mathrm{209}}{\mathrm{54}}} \\ $$$${x}=\frac{\mathrm{4}}{\mathrm{3}}+\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}+\frac{\mathrm{209}}{\mathrm{54}}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{337}}}{\mathrm{6}}−\frac{\mathrm{209}}{\mathrm{54}}}\approx\mathrm{4}.\mathrm{1723} \\ $$
Commented by cortano last updated on 17/Oct/21

$${cardano}\:{by}\:{cortano} \\ $$
