Menu Close

x-3-a-2-x-2-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 105386 by bemath last updated on 28/Jul/20
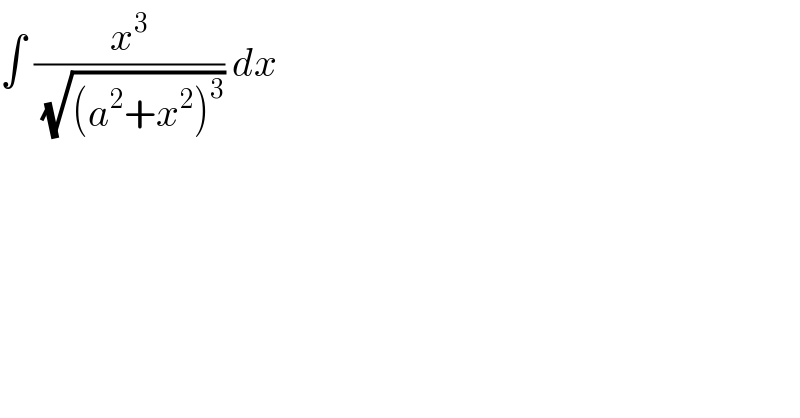
∫ (x^3 /( (√((a^2 +x^2 )^3 )))) dx
$$\int\:\frac{{x}^{\mathrm{3}} }{\:\sqrt{\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:{dx}\: \\ $$
Answered by john santu last updated on 28/Jul/20
by substitute x = a tan θ I= ∫ ((x^3 dx)/( (√((a^2 +x^2 )^3 )))) = a∫ ((tan^3 θ)/(sec^3 θ)).sec^2 θ dθ I= a∫ ((tan^3 θ)/(sec θ))dθ = a∫ ((sin^3 θ)/(cos^2 θ)) dθ set w = cos θ I= −a∫ ((1−w^2 )/w^2 ) dw=aw+(a/w)+c ∴ I=a cos θ+(a/(cos θ))+c I= (a^2 /( (√(a^2 +x^2 )))) + (√(a^2 +x^2 )) + c (JS ♠⧫)
$${by}\:{substitute}\:{x}\:=\:{a}\:\mathrm{tan}\:\theta \\ $$$${I}=\:\int\:\frac{{x}^{\mathrm{3}} {dx}}{\:\sqrt{\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:=\:{a}\int\:\frac{\mathrm{tan}\:^{\mathrm{3}} \theta}{\mathrm{sec}\:^{\mathrm{3}} \theta}.\mathrm{sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$${I}=\:{a}\int\:\frac{\mathrm{tan}\:^{\mathrm{3}} \theta}{\mathrm{sec}\:\theta}{d}\theta\:=\:{a}\int\:\frac{\mathrm{sin}\:^{\mathrm{3}} \theta}{\mathrm{cos}\:^{\mathrm{2}} \theta}\:{d}\theta \\ $$$${set}\:{w}\:=\:\mathrm{cos}\:\theta \\ $$$${I}=\:−{a}\int\:\frac{\mathrm{1}−{w}^{\mathrm{2}} }{{w}^{\mathrm{2}} }\:{dw}={aw}+\frac{{a}}{{w}}+{c} \\ $$$$\therefore\:{I}={a}\:\mathrm{cos}\:\theta+\frac{{a}}{\mathrm{cos}\:\theta}+{c} \\ $$$${I}=\:\frac{{a}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }}\:+\:\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:+\:{c}\: \\ $$$$\left({JS}\:\spadesuit\blacklozenge\right) \\ $$
Answered by mathmax by abdo last updated on 28/Jul/20
I =∫ (x^3 /( (√((a^2 +x^2 )^3 ))))dx we do the changement x =asht ⇒ I =∫ ((a^3 sh^3 t)/( (√(a^6 (cht)^6 )))) ach(t)dt =∫ ((a^3 sh^3 t)/(a^3 ch^3 t)) ×ach(t)dt =a ∫ ((sh^3 t)/(ch^2 t))dt =a ∫ ((sh^2 t sht)/(ch^2 t))dt =a ∫ ((sht(ch^2 t−1))/(ch^2 t))dt =a ∫ sh(t)−a ∫ ((sht)/(ch^2 t))dt =ach(t) +(a/(ch(t))) +c but t =argsh((x/a)) =ln((x/a)+(√(1+(x^2 /a^2 )))) and ch(t) =(√(1+sh^2 t)) =(√(1+(x^2 /a^2 ))) ⇒I =a(√(1+(x^2 /a^2 ))) +(a/( (√(1+(x^2 /a^2 ))))) +C
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{asht}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{a}^{\mathrm{3}} \:\mathrm{sh}^{\mathrm{3}} \mathrm{t}}{\:\sqrt{\mathrm{a}^{\mathrm{6}} \left(\mathrm{cht}\right)^{\mathrm{6}} }}\:\mathrm{ach}\left(\mathrm{t}\right)\mathrm{dt}\:=\int\:\frac{\mathrm{a}^{\mathrm{3}} \:\mathrm{sh}^{\mathrm{3}} \mathrm{t}}{\mathrm{a}^{\mathrm{3}} \mathrm{ch}^{\mathrm{3}} \mathrm{t}}\:×\mathrm{ach}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\mathrm{a}\:\int\:\:\frac{\mathrm{sh}^{\mathrm{3}} \mathrm{t}}{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:=\mathrm{a}\:\int\:\:\frac{\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:\mathrm{sht}}{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:=\mathrm{a}\:\int\:\frac{\mathrm{sht}\left(\mathrm{ch}^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)}{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}\mathrm{dt} \\ $$$$=\mathrm{a}\:\int\:\mathrm{sh}\left(\mathrm{t}\right)−\mathrm{a}\:\int\:\:\frac{\mathrm{sht}}{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}\:=\mathrm{ach}\left(\mathrm{t}\right)\:+\frac{\mathrm{a}}{\mathrm{ch}\left(\mathrm{t}\right)}\:+\mathrm{c} \\ $$$$\mathrm{but}\:\mathrm{t}\:=\mathrm{argsh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)\:\mathrm{and}\:\mathrm{ch}\left(\mathrm{t}\right)\:=\sqrt{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \mathrm{t}} \\ $$$$=\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\:\Rightarrow\mathrm{I}\:=\mathrm{a}\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\:+\frac{\mathrm{a}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}}\:\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *