Question Number 56467 by ajfour last updated on 17/Mar/19
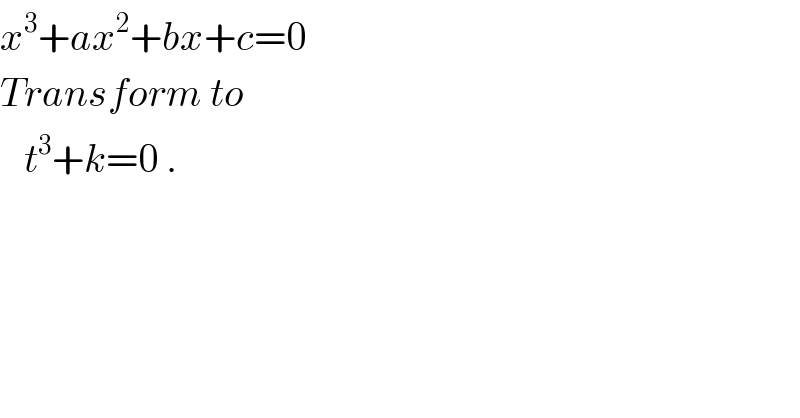
$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${Transform}\:{to}\: \\ $$$$\:\:\:{t}^{\mathrm{3}} +{k}=\mathrm{0}\:. \\ $$
Answered by ajfour last updated on 17/Mar/19
![let x=((pt+q)/(t+1)) ⇒ (pt+q)^3 +a(pt+q)^2 (t+1) +b(pt+q)(t+1)^2 +c(t+1)^3 =0 (p^3 +ap^2 +bp+c)t^3 +(3p^2 q+ap^2 +2apq+bq+2bp+3c)t^2 +(3pq^2 +2apq+aq^2 +bp+2bq+3c)t +q^3 +aq^2 +bq+c=0 Let 3p^2 q+ap^2 +2apq+bq+2bp+3c=0 & 3pq^2 +2apq+aq^2 +bp+2bq+3c=0 subtracting 3pq+a(p+q)−b+2b=0 ⇒ 3pq+a(p+q)+b=0 (i) using this −p[a(p+q)+b]+ap^2 +2apq+bq +2bp+3c = 0 ⇒ apq+bq+bp+3c=0 ⇒ apq+b(p+q)+3c=0 (ii) ⇒ p+q=( determinant ((3,(−b)),(a,(−3c)))/ determinant ((3,a),(a,b)))=((−9c+ab)/(3b−a^2 )) =s ⇒ pq=( determinant (((−b),a),((−3c),b))/ determinant ((3,a),(a,b)))=((−b^2 +3ac)/(3b−a^2 )) =m ⇒ p,q are roots of eq. z^2 −sz+m = 0 z=(s/2)±(√((s^2 /4)−m)) So (p^3 +ap^2 +bp+c)t^3 +q^3 +aq^2 +bq+c = 0 t=−(((q^3 +aq^2 +bq+c)/(p^3 +ap^2 +bp+c)))^(1/3) x=((pt+q)/(t+1)) .](https://www.tinkutara.com/question/Q56472.png)
$${let}\:\:\:{x}=\frac{{pt}+{q}}{{t}+\mathrm{1}}\: \\ $$$$\Rightarrow\:\:\left({pt}+{q}\right)^{\mathrm{3}} +{a}\left({pt}+{q}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:+{b}\left({pt}+{q}\right)\left({t}+\mathrm{1}\right)^{\mathrm{2}} +{c}\left({t}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\left({p}^{\mathrm{3}} +{ap}^{\mathrm{2}} +{bp}+{c}\right){t}^{\mathrm{3}} +\left(\mathrm{3}{p}^{\mathrm{2}} {q}+{ap}^{\mathrm{2}} +\mathrm{2}{apq}+{bq}+\mathrm{2}{bp}+\mathrm{3}{c}\right){t}^{\mathrm{2}} \\ $$$$+\left(\mathrm{3}{pq}^{\mathrm{2}} +\mathrm{2}{apq}+{aq}^{\mathrm{2}} +{bp}+\mathrm{2}{bq}+\mathrm{3}{c}\right){t} \\ $$$$+{q}^{\mathrm{3}} +{aq}^{\mathrm{2}} +{bq}+{c}=\mathrm{0} \\ $$$${Let}\:\:\:\mathrm{3}{p}^{\mathrm{2}} {q}+{ap}^{\mathrm{2}} +\mathrm{2}{apq}+{bq}+\mathrm{2}{bp}+\mathrm{3}{c}=\mathrm{0} \\ $$$$\&\:\:\mathrm{3}{pq}^{\mathrm{2}} +\mathrm{2}{apq}+{aq}^{\mathrm{2}} +{bp}+\mathrm{2}{bq}+\mathrm{3}{c}=\mathrm{0} \\ $$$${subtracting} \\ $$$$\:\:\:\mathrm{3}{pq}+{a}\left({p}+{q}\right)−{b}+\mathrm{2}{b}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{pq}+{a}\left({p}+{q}\right)+{b}=\mathrm{0}\:\:\:\:\left({i}\right) \\ $$$$\:\:{using}\:{this} \\ $$$$\:\:\:−{p}\left[{a}\left({p}+{q}\right)+{b}\right]+{ap}^{\mathrm{2}} +\mathrm{2}{apq}+{bq} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{bp}+\mathrm{3}{c}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{apq}+{bq}+{bp}+\mathrm{3}{c}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{apq}+{b}\left({p}+{q}\right)+\mathrm{3}{c}=\mathrm{0}\:\:\:\:\left({ii}\right) \\ $$$$\Rightarrow\:\:{p}+{q}=\frac{\begin{vmatrix}{\mathrm{3}}&{−{b}}\\{{a}}&{−\mathrm{3}{c}}\end{vmatrix}}{\begin{vmatrix}{\mathrm{3}}&{{a}}\\{{a}}&{{b}}\end{vmatrix}}=\frac{−\mathrm{9}{c}+{ab}}{\mathrm{3}{b}−{a}^{\mathrm{2}} }\:={s} \\ $$$$\Rightarrow\:\:\:{pq}=\frac{\begin{vmatrix}{−{b}}&{{a}}\\{−\mathrm{3}{c}}&{{b}}\end{vmatrix}}{\begin{vmatrix}{\mathrm{3}}&{{a}}\\{{a}}&{{b}}\end{vmatrix}}=\frac{−{b}^{\mathrm{2}} +\mathrm{3}{ac}}{\mathrm{3}{b}−{a}^{\mathrm{2}} }\:={m} \\ $$$$\Rightarrow\:{p},{q}\:{are}\:{roots}\:{of}\:{eq}. \\ $$$$\:\:\:\:{z}^{\mathrm{2}} −{sz}+{m}\:=\:\mathrm{0} \\ $$$$\:\:{z}=\frac{{s}}{\mathrm{2}}\pm\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{4}}−{m}} \\ $$$${So} \\ $$$$\:\:\:\:\left({p}^{\mathrm{3}} +{ap}^{\mathrm{2}} +{bp}+{c}\right){t}^{\mathrm{3}} +{q}^{\mathrm{3}} +{aq}^{\mathrm{2}} +{bq}+{c}\:=\:\mathrm{0} \\ $$$$\:{t}=−\left(\frac{{q}^{\mathrm{3}} +{aq}^{\mathrm{2}} +{bq}+{c}}{{p}^{\mathrm{3}} +{ap}^{\mathrm{2}} +{bp}+{c}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:{x}=\frac{{pt}+{q}}{{t}+\mathrm{1}}\:. \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 17/Mar/19
![let try for: [x^3 +2x^2 +3x+4=0] {a=2,b=3,c=4} p+q=((−9c+ab)/(3b−a^2 ))=((−9×4+2×3)/(9−4))=−6 pq=((−b^2 +3ac)/(3b−a^2 ))=((−9+3×2×4)/5)=+3 ⇒z^2 +6z+3=0⇒z=((−6±(√(36−12)))/2)= ⇒z=−3±(√6)⇒ { ((p=−3+(√6)=−0.55,q=−3−(√6)=−5.44)),((p=−3−(√6),q=−3+(√6))) :} t^3 =−((q^3 +aq^2 +bq+c)/(p^3 +ap^2 +bp+c))=−(((−5.44)^3 +2(−5.44)^2 +3(−5.44)+4)/((−0.55)^3 +2(−0.55)^2 +3(−0.55)+4))=40.924 t=(40.925)^(1/3) =3.446 x=((pt+q)/(t+1))=((−0.55×3.446−5.44)/(3.446+1))=−1.65[ok!]](https://www.tinkutara.com/question/Q56506.png)
$${let}\:{try}\:{for}:\:\:\:\left[\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{4}=\mathrm{0}\right] \\ $$$$\left\{{a}=\mathrm{2},{b}=\mathrm{3},{c}=\mathrm{4}\right\} \\ $$$${p}+{q}=\frac{−\mathrm{9}{c}+{ab}}{\mathrm{3}{b}−{a}^{\mathrm{2}} }=\frac{−\mathrm{9}×\mathrm{4}+\mathrm{2}×\mathrm{3}}{\mathrm{9}−\mathrm{4}}=−\mathrm{6} \\ $$$${pq}=\frac{−{b}^{\mathrm{2}} +\mathrm{3}{ac}}{\mathrm{3}{b}−{a}^{\mathrm{2}} }=\frac{−\mathrm{9}+\mathrm{3}×\mathrm{2}×\mathrm{4}}{\mathrm{5}}=+\mathrm{3} \\ $$$$\Rightarrow{z}^{\mathrm{2}} +\mathrm{6}{z}+\mathrm{3}=\mathrm{0}\Rightarrow{z}=\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{12}}}{\mathrm{2}}= \\ $$$$\Rightarrow{z}=−\mathrm{3}\pm\sqrt{\mathrm{6}}\Rightarrow\begin{cases}{{p}=−\mathrm{3}+\sqrt{\mathrm{6}}=−\mathrm{0}.\mathrm{55},{q}=−\mathrm{3}−\sqrt{\mathrm{6}}=−\mathrm{5}.\mathrm{44}}\\{{p}=−\mathrm{3}−\sqrt{\mathrm{6}},{q}=−\mathrm{3}+\sqrt{\mathrm{6}}}\end{cases} \\ $$$${t}^{\mathrm{3}} =−\frac{{q}^{\mathrm{3}} +{aq}^{\mathrm{2}} +{bq}+{c}}{{p}^{\mathrm{3}} +{ap}^{\mathrm{2}} +{bp}+{c}}=−\frac{\left(−\mathrm{5}.\mathrm{44}\right)^{\mathrm{3}} +\mathrm{2}\left(−\mathrm{5}.\mathrm{44}\right)^{\mathrm{2}} +\mathrm{3}\left(−\mathrm{5}.\mathrm{44}\right)+\mathrm{4}}{\left(−\mathrm{0}.\mathrm{55}\right)^{\mathrm{3}} +\mathrm{2}\left(−\mathrm{0}.\mathrm{55}\right)^{\mathrm{2}} +\mathrm{3}\left(−\mathrm{0}.\mathrm{55}\right)+\mathrm{4}}=\mathrm{40}.\mathrm{924} \\ $$$${t}=\left(\mathrm{40}.\mathrm{925}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{3}.\mathrm{446} \\ $$$${x}=\frac{{pt}+{q}}{{t}+\mathrm{1}}=\frac{−\mathrm{0}.\mathrm{55}×\mathrm{3}.\mathrm{446}−\mathrm{5}.\mathrm{44}}{\mathrm{3}.\mathrm{446}+\mathrm{1}}=−\mathrm{1}.\mathrm{65}\left[\boldsymbol{{ok}}!\right] \\ $$
Commented by mr W last updated on 17/Mar/19
��������
Commented by behi83417@gmail.com last updated on 17/Mar/19

Commented by behi83417@gmail.com last updated on 17/Mar/19

$${congratulations}\:{sir}\:{Ajfour}! \\ $$$${this}\:{is}\:{a}\:{perfect}\:{way}\:{for}\:\mathrm{3}{rd}\:{deg}.{eq} \\ $$$${thanks}\:{for}\:{sharing}\:{this}\:{knowledges}. \\ $$
