x-3-ax-b-dx-

Question Number 123964 by mindispower last updated on 29/Nov/20

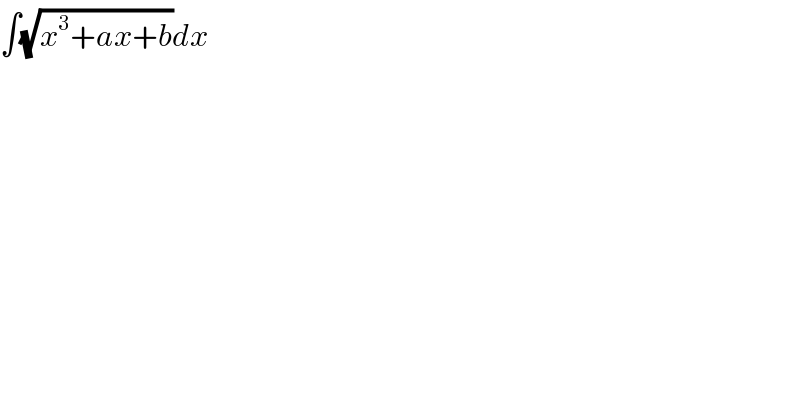
$$\int\sqrt{{x}^{\mathrm{3}} +{ax}+{b}}{dx} \\ $$

Commented by MJS_new last updated on 29/Nov/20

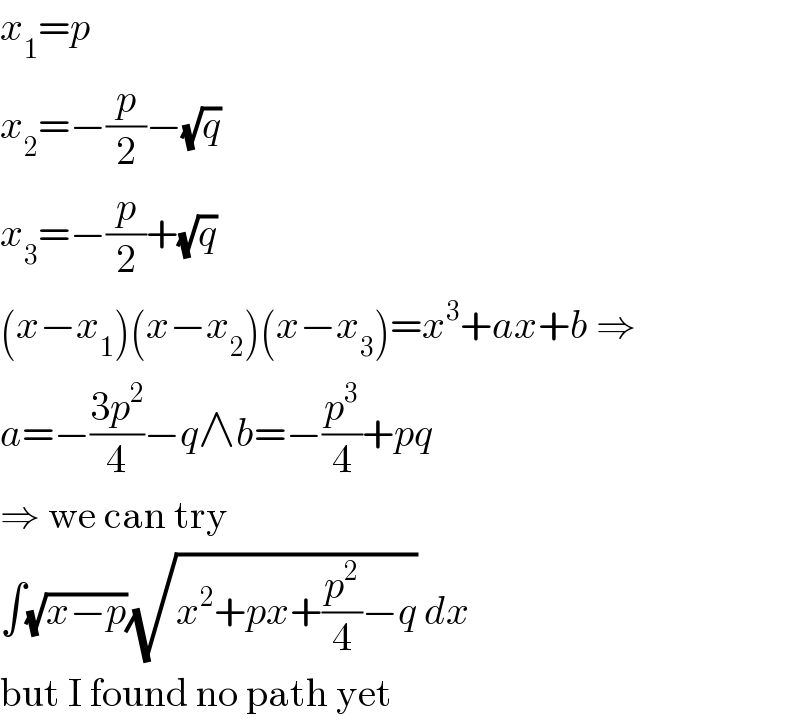
x_1 =p x_2 =−(p/2)−(√q) x_3 =−(p/2)+(√q) (x−x_1 )(x−x_2 )(x−x_3 )=x^3 +ax+b ⇒ a=−((3p^2 )/4)−q∧b=−(p^3 /4)+pq ⇒ we can try ∫(√(x−p))(√(x^2 +px+(p^2 /4)−q)) dx but I found no path yet

$${x}_{\mathrm{1}} ={p} \\ $$$${x}_{\mathrm{2}} =−\frac{{p}}{\mathrm{2}}−\sqrt{{q}} \\ $$$${x}_{\mathrm{3}} =−\frac{{p}}{\mathrm{2}}+\sqrt{{q}} \\ $$$$\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)\left({x}−{x}_{\mathrm{3}} \right)={x}^{\mathrm{3}} +{ax}+{b}\:\Rightarrow \\ $$$${a}=−\frac{\mathrm{3}{p}^{\mathrm{2}} }{\mathrm{4}}−{q}\wedge{b}=−\frac{{p}^{\mathrm{3}} }{\mathrm{4}}+{pq} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{try} \\ $$$$\int\sqrt{{x}−{p}}\sqrt{{x}^{\mathrm{2}} +{px}+\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}}\:{dx} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{path}\:\mathrm{yet} \\ $$

Commented by mindispower last updated on 30/Nov/20

thank you sir me too i have not found somthing my bee there is no close]form or some special function we dont see yet have a nice day sir

$${thank}\:{you}\:{sir}\:{me}\:{too}\:{i}\:{have}\:{not}\:{found}\:{somthing} \\ $$$$\left.{my}\:{bee}\:{there}\:{is}\:{no}\:{close}\right]{form}\:{or}\: \\ $$$${some}\:{special}\:{function}\:{we}\:{dont}\:{see}\:{yet} \\ $$$${have}\:{a}\:{nice}\:{day}\:{sir}\: \\ $$$$ \\ $$

Commented by MJS_new last updated on 30/Nov/20

Wolfram Alpha gives super complicated solutions for ∫(√(x−p))(√(x^2 +px+(p^2 /4)−q)) dx and∫(√(x−p))(√(x+(p/2)−(√q)))(√(x+(p/2)+(√q))) dx, (for ∫(√(x^3 +ax+b)) dx it′s also including the terms “root #n”with n=1, 2, 3) including elliptic functions E and F; but it cannot solve ∫(√(x−a))(√(x−b))(√(x−c)) at all.

$$\mathrm{Wolfram}\:\mathrm{Alpha}\:\mathrm{gives}\:\mathrm{super}\:\mathrm{complicated} \\ $$$$\mathrm{solutions}\:\mathrm{for}\:\int\sqrt{{x}−{p}}\sqrt{{x}^{\mathrm{2}} +{px}+\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}}\:{dx} \\ $$$$\mathrm{and}\int\sqrt{{x}−{p}}\sqrt{{x}+\frac{{p}}{\mathrm{2}}−\sqrt{{q}}}\sqrt{{x}+\frac{{p}}{\mathrm{2}}+\sqrt{{q}}}\:{dx}, \\ $$$$\left(\mathrm{for}\:\int\sqrt{{x}^{\mathrm{3}} +{ax}+{b}}\:{dx}\:\mathrm{it}'\mathrm{s}\:\mathrm{also}\:\mathrm{including}\:\mathrm{the}\right. \\ $$$$\left.\mathrm{terms}\:“\mathrm{root}\:#{n}''\mathrm{with}\:{n}=\mathrm{1},\:\mathrm{2},\:\mathrm{3}\right) \\ $$$$\mathrm{including}\:\mathrm{elliptic}\:\mathrm{functions}\:\mathrm{E}\:\mathrm{and}\:\mathrm{F};\:\mathrm{but}\:\mathrm{it} \\ $$$$\mathrm{cannot}\:\mathrm{solve}\:\int\sqrt{{x}−{a}}\sqrt{{x}−{b}}\sqrt{{x}−{c}}\:\mathrm{at}\:\mathrm{all}. \\ $$

Commented by mindispower last updated on 30/Nov/20

thank you sir i see ∫(√(x−a)).(√(x^2 +_− b)) can bee solved by x=(√b)ch(t),wehen − x=(√b)sh(t),when + may bee thanx again sir x=

$${thank}\:{you}\:{sir}\: \\ $$$${i}\:{see}\: \\ $$$$\int\sqrt{{x}−{a}}.\sqrt{{x}^{\mathrm{2}} \underset{−} {+}{b}} \\ $$$${can}\:{bee}\:{solved}\:{by} \\ $$$${x}=\sqrt{{b}}{ch}\left({t}\right),{wehen}\:\:− \\ $$$${x}=\sqrt{{b}}{sh}\left({t}\right),{when}\:+\:{may}\:{bee} \\ $$$${thanx}\:{again}\:{sir} \\ $$$${x}= \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply