Menu Close

x-3-bx-c-0-b-c-gt-0-b-3-3-gt-c-2-2-To-find-the-three-real-roots-without-the-use-of-trigonometric-solution-to-cubic-polynomial-

Tinku Tara 0 Comments
Pin




Question Number 102490 by ajfour last updated on 09/Jul/20
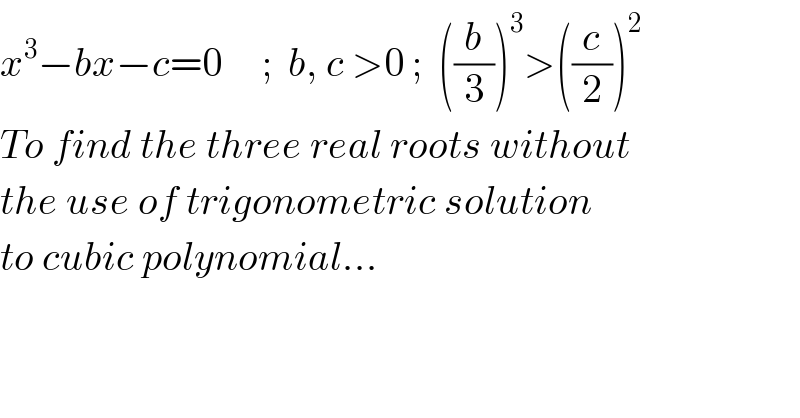
x^3 −bx−c=0 ; b, c >0 ; ((b/3))^3 >((c/2))^2 To find the three real roots without the use of trigonometric solution to cubic polynomial...
$${x}^{\mathrm{3}} −{bx}−{c}=\mathrm{0}\:\:\:\:\:;\:\:{b},\:{c}\:>\mathrm{0}\:;\:\:\left(\frac{{b}}{\mathrm{3}}\right)^{\mathrm{3}} >\left(\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${To}\:{find}\:{the}\:{three}\:{real}\:{roots}\:{without} \\ $$$${the}\:{use}\:{of}\:{trigonometric}\:{solution} \\ $$$${to}\:{cubic}\:{polynomial}… \\ $$
Answered by ajfour last updated on 10/Jul/20
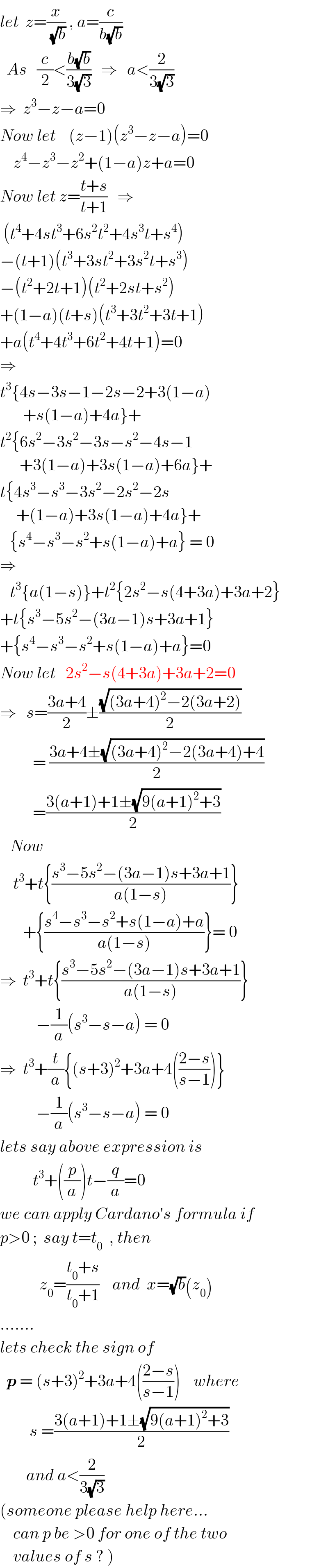
let z=(x/( (√b))) , a=(c/(b(√b))) As (c/2)<((b(√b))/(3(√3))) ⇒ a<(2/(3(√3))) ⇒ z^3 −z−a=0 Now let (z−1)(z^3 −z−a)=0 z^4 −z^3 −z^2 +(1−a)z+a=0 Now let z=((t+s)/(t+1)) ⇒ (t^4 +4st^3 +6s^2 t^2 +4s^3 t+s^4 ) −(t+1)(t^3 +3st^2 +3s^2 t+s^3 ) −(t^2 +2t+1)(t^2 +2st+s^2 ) +(1−a)(t+s)(t^3 +3t^2 +3t+1) +a(t^4 +4t^3 +6t^2 +4t+1)=0 ⇒ t^3 {4s−3s−1−2s−2+3(1−a) +s(1−a)+4a}+ t^2 {6s^2 −3s^2 −3s−s^2 −4s−1 +3(1−a)+3s(1−a)+6a}+ t{4s^3 −s^3 −3s^2 −2s^2 −2s +(1−a)+3s(1−a)+4a}+ {s^4 −s^3 −s^2 +s(1−a)+a} = 0 ⇒ t^3 {a(1−s)}+t^2 {2s^2 −s(4+3a)+3a+2} +t{s^3 −5s^2 −(3a−1)s+3a+1} +{s^4 −s^3 −s^2 +s(1−a)+a}=0 Now let 2s^2 −s(4+3a)+3a+2=0 ⇒ s=((3a+4)/2)±((√((3a+4)^2 −2(3a+2)))/2) = ((3a+4±(√((3a+4)^2 −2(3a+4)+4)))/2) =((3(a+1)+1±(√(9(a+1)^2 +3)))/2) Now t^3 +t{((s^3 −5s^2 −(3a−1)s+3a+1)/(a(1−s)))} +{((s^4 −s^3 −s^2 +s(1−a)+a)/(a(1−s)))}= 0 ⇒ t^3 +t{((s^3 −5s^2 −(3a−1)s+3a+1)/(a(1−s)))} −(1/a)(s^3 −s−a) = 0 ⇒ t^3 +(t/a){(s+3)^2 +3a+4(((2−s)/(s−1)))} −(1/a)(s^3 −s−a) = 0 lets say above expression is t^3 +((p/a))t−(q/a)=0 we can apply Cardano′s formula if p>0 ; say t=t_0 , then z_0 =((t_0 +s)/(t_0 +1)) and x=(√b)(z_0 ) ....... lets check the sign of p = (s+3)^2 +3a+4(((2−s)/(s−1))) where s =((3(a+1)+1±(√(9(a+1)^2 +3)))/2) and a<(2/(3(√3))) (someone please help here... can p be >0 for one of the two values of s ? )
$${let}\:\:{z}=\frac{{x}}{\:\sqrt{{b}}}\:,\:{a}=\frac{{c}}{{b}\sqrt{{b}}} \\ $$$$\:\:{As}\:\:\:\frac{{c}}{\mathrm{2}}<\frac{{b}\sqrt{{b}}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\:\:\Rightarrow\:\:\:{a}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:{z}^{\mathrm{3}} −{z}−{a}=\mathrm{0} \\ $$$${Now}\:{let}\:\:\:\:\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{3}} −{z}−{a}\right)=\mathrm{0} \\ $$$$\:\:\:\:{z}^{\mathrm{4}} −{z}^{\mathrm{3}} −{z}^{\mathrm{2}} +\left(\mathrm{1}−{a}\right){z}+{a}=\mathrm{0} \\ $$$${Now}\:{let}\:{z}=\frac{{t}+{s}}{{t}+\mathrm{1}}\:\:\:\Rightarrow \\ $$$$\:\left({t}^{\mathrm{4}} +\mathrm{4}{st}^{\mathrm{3}} +\mathrm{6}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{4}{s}^{\mathrm{3}} {t}+{s}^{\mathrm{4}} \right) \\ $$$$−\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{3}} +\mathrm{3}{st}^{\mathrm{2}} +\mathrm{3}{s}^{\mathrm{2}} {t}+{s}^{\mathrm{3}} \right) \\ $$$$−\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{st}+{s}^{\mathrm{2}} \right) \\ $$$$+\left(\mathrm{1}−{a}\right)\left({t}+{s}\right)\left({t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{1}\right) \\ $$$$+{a}\left({t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{3}} \left\{\mathrm{4}{s}−\mathrm{3}{s}−\mathrm{1}−\mathrm{2}{s}−\mathrm{2}+\mathrm{3}\left(\mathrm{1}−{a}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:+{s}\left(\mathrm{1}−{a}\right)+\mathrm{4}{a}\right\}+ \\ $$$${t}^{\mathrm{2}} \left\{\mathrm{6}{s}^{\mathrm{2}} −\mathrm{3}{s}^{\mathrm{2}} −\mathrm{3}{s}−{s}^{\mathrm{2}} −\mathrm{4}{s}−\mathrm{1}\right. \\ $$$$\left.\:\:\:\:\:\:+\mathrm{3}\left(\mathrm{1}−{a}\right)+\mathrm{3}{s}\left(\mathrm{1}−{a}\right)+\mathrm{6}{a}\right\}+ \\ $$$${t}\left\{\mathrm{4}{s}^{\mathrm{3}} −{s}^{\mathrm{3}} −\mathrm{3}{s}^{\mathrm{2}} −\mathrm{2}{s}^{\mathrm{2}} −\mathrm{2}{s}\right. \\ $$$$\left.\:\:\:\:\:+\left(\mathrm{1}−{a}\right)+\mathrm{3}{s}\left(\mathrm{1}−{a}\right)+\mathrm{4}{a}\right\}+ \\ $$$$\:\:\:\left\{{s}^{\mathrm{4}} −{s}^{\mathrm{3}} −{s}^{\mathrm{2}} +{s}\left(\mathrm{1}−{a}\right)+{a}\right\}\:=\:\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\:\:{t}^{\mathrm{3}} \left\{{a}\left(\mathrm{1}−{s}\right)\right\}+{t}^{\mathrm{2}} \left\{\mathrm{2}{s}^{\mathrm{2}} −{s}\left(\mathrm{4}+\mathrm{3}{a}\right)+\mathrm{3}{a}+\mathrm{2}\right\} \\ $$$$+{t}\left\{{s}^{\mathrm{3}} −\mathrm{5}{s}^{\mathrm{2}} −\left(\mathrm{3}{a}−\mathrm{1}\right){s}+\mathrm{3}{a}+\mathrm{1}\right\} \\ $$$$+\left\{{s}^{\mathrm{4}} −{s}^{\mathrm{3}} −{s}^{\mathrm{2}} +{s}\left(\mathrm{1}−{a}\right)+{a}\right\}=\mathrm{0} \\ $$$${Now}\:{let}\:\:\:\mathrm{2}{s}^{\mathrm{2}} −{s}\left(\mathrm{4}+\mathrm{3}{a}\right)+\mathrm{3}{a}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{s}=\frac{\mathrm{3}{a}+\mathrm{4}}{\mathrm{2}}\pm\frac{\sqrt{\left(\mathrm{3}{a}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}{a}+\mathrm{2}\right)}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{3}{a}+\mathrm{4}\pm\sqrt{\left(\mathrm{3}{a}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}{a}+\mathrm{4}\right)+\mathrm{4}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}\left({a}+\mathrm{1}\right)+\mathrm{1}\pm\sqrt{\mathrm{9}\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:{Now}\:\:\: \\ $$$$\:\:\:\:{t}^{\mathrm{3}} +{t}\left\{\frac{{s}^{\mathrm{3}} −\mathrm{5}{s}^{\mathrm{2}} −\left(\mathrm{3}{a}−\mathrm{1}\right){s}+\mathrm{3}{a}+\mathrm{1}}{{a}\left(\mathrm{1}−{s}\right)}\right\} \\ $$$$\:\:\:\:\:\:\:+\left\{\frac{{s}^{\mathrm{4}} −{s}^{\mathrm{3}} −{s}^{\mathrm{2}} +{s}\left(\mathrm{1}−{a}\right)+{a}}{{a}\left(\mathrm{1}−{s}\right)}\right\}=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} +{t}\left\{\frac{{s}^{\mathrm{3}} −\mathrm{5}{s}^{\mathrm{2}} −\left(\mathrm{3}{a}−\mathrm{1}\right){s}+\mathrm{3}{a}+\mathrm{1}}{{a}\left(\mathrm{1}−{s}\right)}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{{a}}\left({s}^{\mathrm{3}} −{s}−{a}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} +\frac{{t}}{{a}}\left\{\left({s}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{4}\left(\frac{\mathrm{2}−{s}}{{s}−\mathrm{1}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{{a}}\left({s}^{\mathrm{3}} −{s}−{a}\right)\:=\:\mathrm{0} \\ $$$${lets}\:{say}\:{above}\:{expression}\:{is} \\ $$$$\:\:\:\:\:\:\:\:\:\:{t}^{\mathrm{3}} +\left(\frac{{p}}{{a}}\right){t}−\frac{{q}}{{a}}=\mathrm{0} \\ $$$${we}\:{can}\:{apply}\:{Cardano}'{s}\:{formula}\:{if} \\ $$$${p}>\mathrm{0}\:;\:\:{say}\:{t}={t}_{\mathrm{0}} \:\:,\:{then} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{z}_{\mathrm{0}} =\frac{{t}_{\mathrm{0}} +{s}}{{t}_{\mathrm{0}} +\mathrm{1}}\:\:\:\:{and}\:\:{x}=\sqrt{{b}}\left({z}_{\mathrm{0}} \right) \\ $$$$……. \\ $$$${lets}\:{check}\:{the}\:{sign}\:{of}\: \\ $$$$\:\:\boldsymbol{{p}}\:=\:\left({s}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{3}{a}+\mathrm{4}\left(\frac{\mathrm{2}−{s}}{{s}−\mathrm{1}}\right)\:\:\:\:{where} \\ $$$$\:\:\:\:\:\:\:\:\:{s}\:=\frac{\mathrm{3}\left({a}+\mathrm{1}\right)+\mathrm{1}\pm\sqrt{\mathrm{9}\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{and}\:{a}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\left({someone}\:{please}\:{help}\:{here}…\right. \\ $$$$\:\:\:\:{can}\:{p}\:{be}\:>\mathrm{0}\:{for}\:{one}\:{of}\:{the}\:{two} \\ $$$$\left.\:\:\:\:{values}\:{of}\:{s}\:?\:\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *