Question Number 92398 by jagoll last updated on 06/May/20
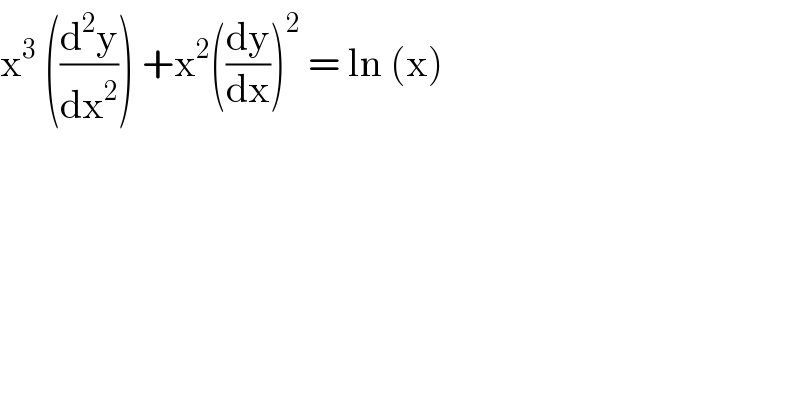
$$\mathrm{x}^{\mathrm{3}} \:\left(\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\right)\:+\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \:=\:\mathrm{ln}\:\left(\mathrm{x}\right)\: \\ $$
Answered by Joel578 last updated on 06/May/20
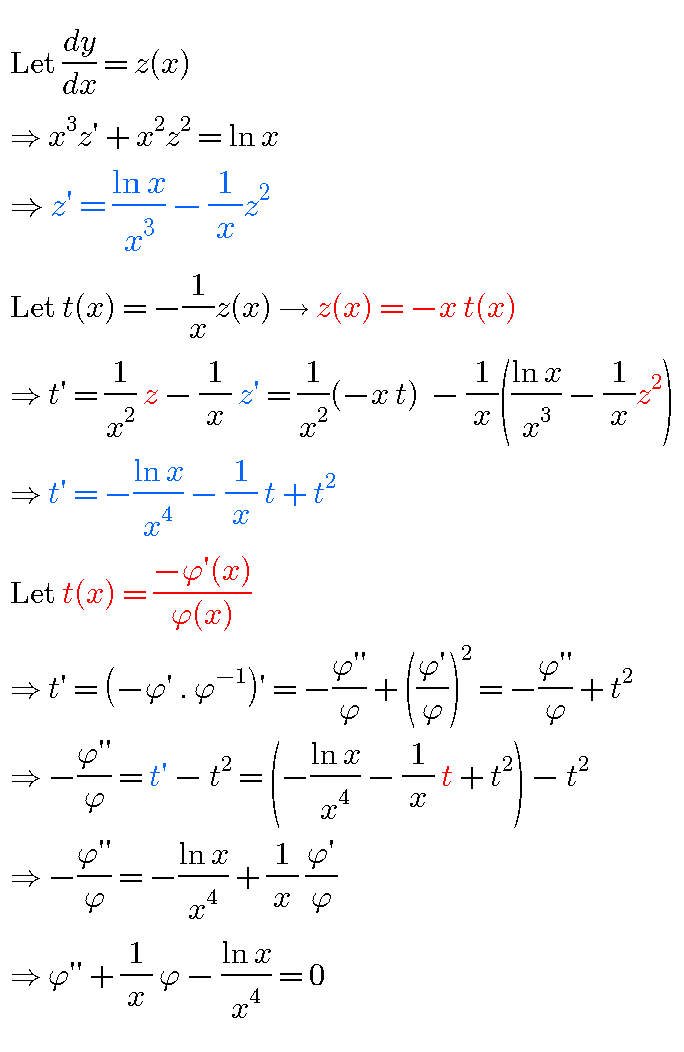
Commented by Joel578 last updated on 06/May/20
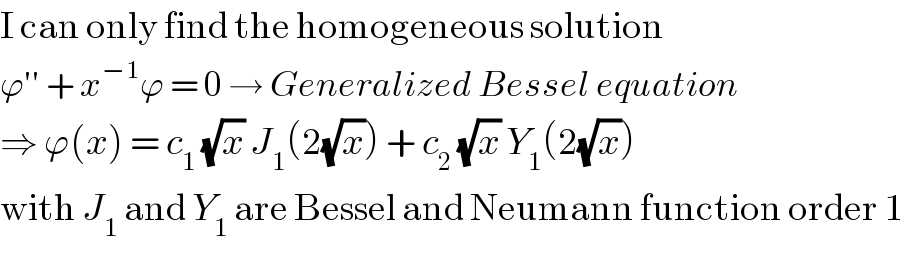
$$\mathrm{I}\:\mathrm{can}\:\mathrm{only}\:\mathrm{find}\:\mathrm{the}\:\mathrm{homogeneous}\:\mathrm{solution} \\ $$$$\varphi''\:+\:{x}^{−\mathrm{1}} \varphi\:=\:\mathrm{0}\:\rightarrow\:{Generalized}\:{Bessel}\:{equation} \\ $$$$\Rightarrow\:\varphi\left({x}\right)\:=\:{c}_{\mathrm{1}} \:\sqrt{{x}}\:{J}_{\mathrm{1}} \left(\mathrm{2}\sqrt{{x}}\right)\:+\:{c}_{\mathrm{2}} \:\sqrt{{x}}\:{Y}_{\mathrm{1}} \left(\mathrm{2}\sqrt{{x}}\right) \\ $$$$\mathrm{with}\:{J}_{\mathrm{1}} \:\mathrm{and}\:{Y}_{\mathrm{1}} \:\mathrm{are}\:\mathrm{Bessel}\:\mathrm{and}\:\mathrm{Neumann}\:\mathrm{function}\:\mathrm{order}\:\mathrm{1} \\ $$
Commented by Joel578 last updated on 06/May/20

$$\mathrm{Maybe}\:\mathrm{someone}\:\mathrm{knows}\:\mathrm{a}\:\mathrm{better}\:\mathrm{method}\:\mathrm{to} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{diff}\:\mathrm{equation} \\ $$
