Question Number 180894 by depressiveshrek last updated on 18/Nov/22

$${x}^{\mathrm{3}} +{x}=\mathrm{1} \\ $$$${x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} =? \\ $$
Commented by Rasheed.Sindhi last updated on 19/Nov/22

$$\mathcal{T}{he}\:{solutions}/{answers}\:\left({complete}\right. \\ $$$$\left.{process}\right)\:{should}\:{be}\:{posted}\:{as}\:“\mathrm{Answer}'' \\ $$$${not}\:{as}\:{comment}\:\left({kindly}\right). \\ $$
Commented by Gamil last updated on 19/Nov/22
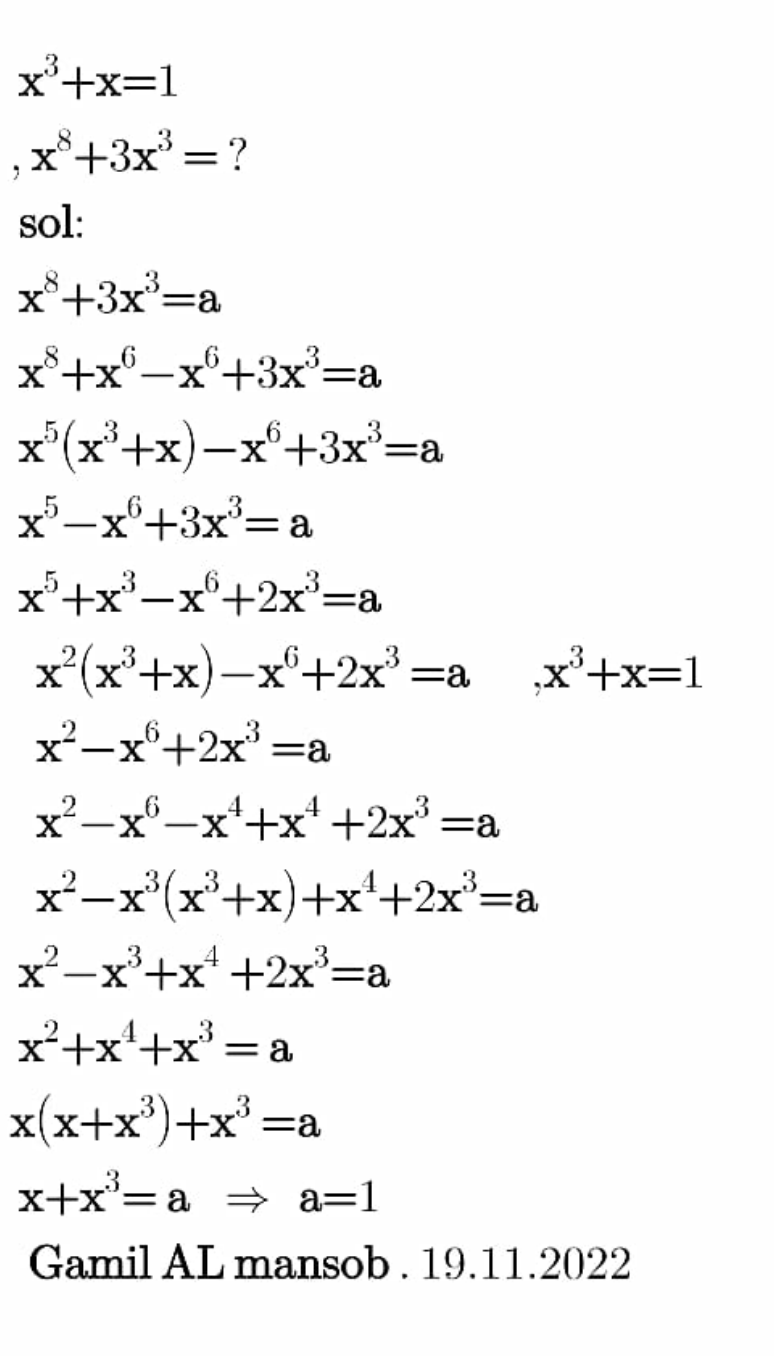
Answered by Frix last updated on 18/Nov/22
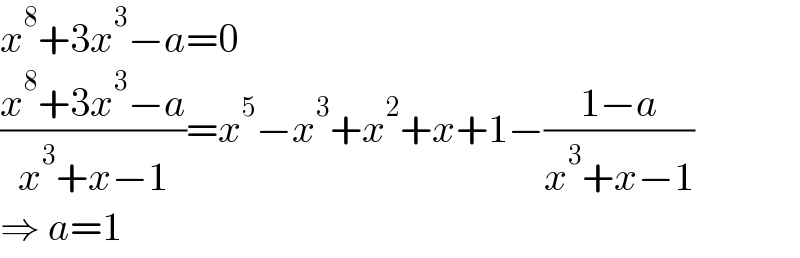
$${x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} −{a}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} −{a}}{{x}^{\mathrm{3}} +{x}−\mathrm{1}}={x}^{\mathrm{5}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}−\frac{\mathrm{1}−{a}}{{x}^{\mathrm{3}} +{x}−\mathrm{1}} \\ $$$$\Rightarrow\:{a}=\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 19/Nov/22
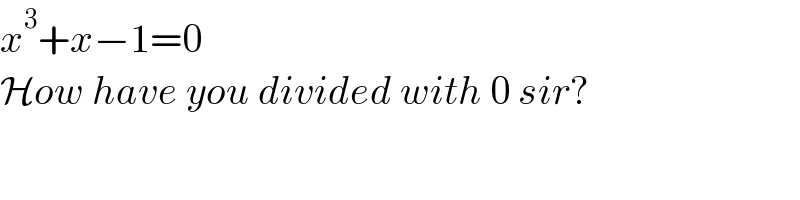
$${x}^{\mathrm{3}} +{x}−\mathrm{1}=\mathrm{0}\: \\ $$$$\mathcal{H}{ow}\:{have}\:{you}\:{divided}\:{with}\:\mathrm{0}\:{sir}? \\ $$
Commented by Frix last updated on 19/Nov/22
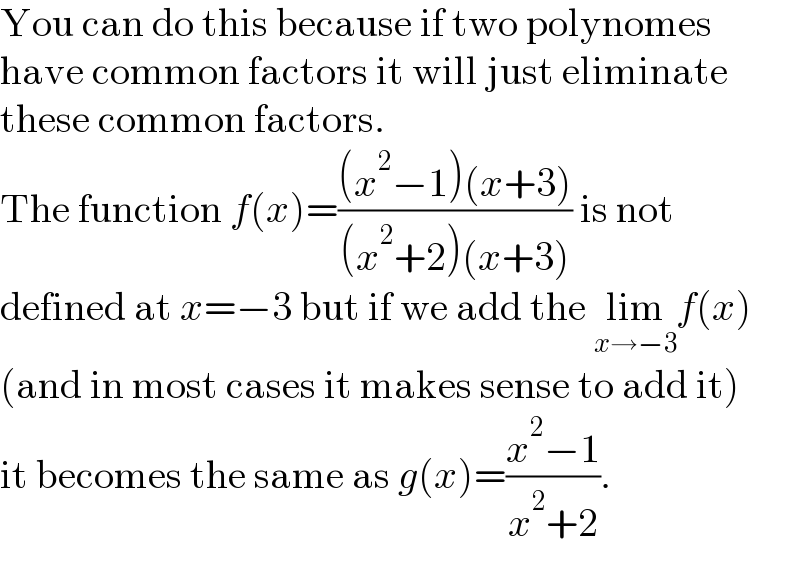
$$\mathrm{You}\:\mathrm{can}\:\mathrm{do}\:\mathrm{this}\:\mathrm{because}\:\mathrm{if}\:\mathrm{two}\:\mathrm{polynomes} \\ $$$$\mathrm{have}\:\mathrm{common}\:\mathrm{factors}\:\mathrm{it}\:\mathrm{will}\:\mathrm{just}\:\mathrm{eliminate} \\ $$$$\mathrm{these}\:\mathrm{common}\:\mathrm{factors}. \\ $$$$\mathrm{The}\:\mathrm{function}\:{f}\left({x}\right)=\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}+\mathrm{3}\right)}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}+\mathrm{3}\right)}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{defined}\:\mathrm{at}\:{x}=−\mathrm{3}\:\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{add}\:\mathrm{the}\:\underset{{x}\rightarrow−\mathrm{3}} {\mathrm{lim}}{f}\left({x}\right) \\ $$$$\left(\mathrm{and}\:\mathrm{in}\:\mathrm{most}\:\mathrm{cases}\:\mathrm{it}\:\mathrm{makes}\:\mathrm{sense}\:\mathrm{to}\:\mathrm{add}\:\mathrm{it}\right) \\ $$$$\mathrm{it}\:\mathrm{becomes}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:{g}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}. \\ $$
Commented by Rasheed.Sindhi last updated on 19/Nov/22

$$\mathcal{T}{han}\mathcal{X}\:\boldsymbol{{sir}}! \\ $$
Answered by Rasheed.Sindhi last updated on 19/Nov/22
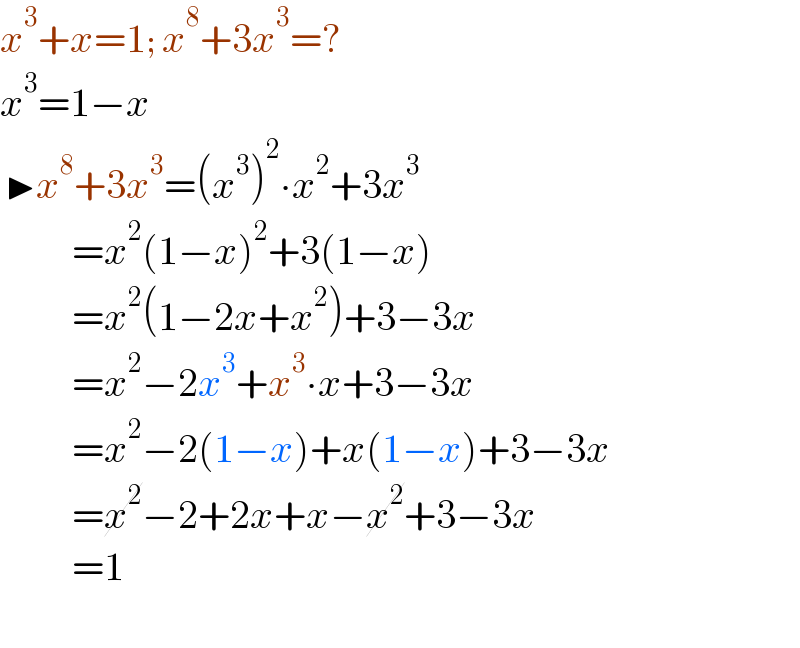
$${x}^{\mathrm{3}} +{x}=\mathrm{1};\:{x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} =? \\ $$$${x}^{\mathrm{3}} =\mathrm{1}−{x} \\ $$$$\:\blacktriangleright{x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} =\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} \centerdot{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)+\mathrm{3}−\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{3}} \centerdot{x}+\mathrm{3}−\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−{x}\right)+{x}\left(\mathrm{1}−{x}\right)+\mathrm{3}−\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:\:\:=\cancel{{x}^{\mathrm{2}} }−\mathrm{2}+\mathrm{2}{x}+{x}−\cancel{{x}^{\mathrm{2}} }+\mathrm{3}−\mathrm{3}{x} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by mr W last updated on 19/Nov/22
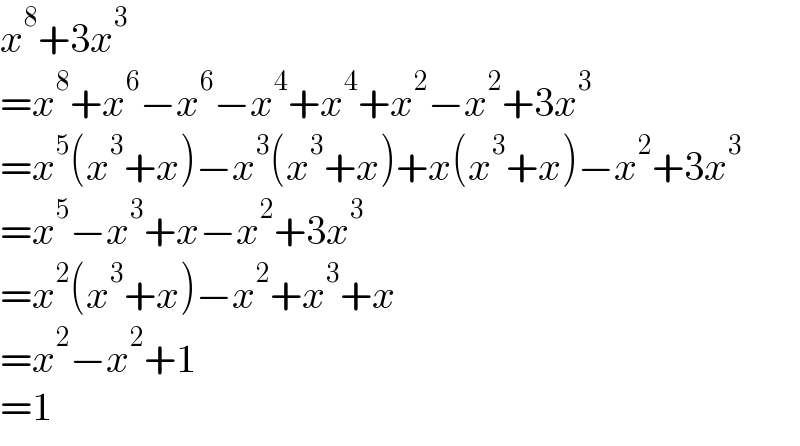
$${x}^{\mathrm{8}} +\mathrm{3}{x}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{8}} +{x}^{\mathrm{6}} −{x}^{\mathrm{6}} −{x}^{\mathrm{4}} +{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{5}} \left({x}^{\mathrm{3}} +{x}\right)−{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} +{x}\right)+{x}\left({x}^{\mathrm{3}} +{x}\right)−{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{5}} −{x}^{\mathrm{3}} +{x}−{x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{3}} \\ $$$$={x}^{\mathrm{2}} \left({x}^{\mathrm{3}} +{x}\right)−{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x} \\ $$$$={x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$=\mathrm{1} \\ $$
