Menu Close

x-3-x-16-0-

Tinku Tara 0 Comments
Pin




Question Number 89687 by student work last updated on 18/Apr/20
x^3 +x−16=0
$${x}^{\mathrm{3}} +{x}−\mathrm{16}=\mathrm{0} \\ $$
Commented by mr W last updated on 18/Apr/20
https://en.m.wikipedia.org/wiki/Cubic_equation
Commented by mr W last updated on 18/Apr/20
it′s already solved in Q89653. method is also told you. have you tried to study the method? if you just want to know the formula, you can find it in internet. if you want to understand it, you should study it through some reading by yourself.
$${it}'{s}\:{already}\:{solved}\:{in}\:{Q}\mathrm{89653}. \\ $$$${method}\:{is}\:{also}\:{told}\:{you}.\:{have}\:{you}\:{tried} \\ $$$${to}\:{study}\:{the}\:{method}?\:{if}\:{you}\:{just}\:{want} \\ $$$${to}\:{know}\:{the}\:{formula},\:{you}\:{can}\:{find}\:{it} \\ $$$${in}\:{internet}.\:{if}\:{you}\:{want}\:{to}\:{understand} \\ $$$${it},\:{you}\:{should}\:{study}\:{it}\:{through}\:{some} \\ $$$${reading}\:{by}\:{yourself}. \\ $$
Commented by MJS last updated on 18/Apr/20
Cardano′s Method ax^3 +bx^2 +cx+d=0 (1) divide by a ⇒ x^3 +(b/a)x^2 +(c/a)x+(d/a)=0 (2) let z=x−(b/(3a)) ⇒ z^3 +((3ac−b^2 )/(3a^2 ))z+((27a^2 d−9abc+2b^3 )/(27a^3 ))=0 (3) let ((3ac−b^2 )/(3a^2 ))=p and ((27a^2 d−9abc+2b^3 )/(27a^3 ))=q ⇒ z^3 +pz+q=0 ⇔ z^3 =−pz−q (4) Cardano′s new idea: let z=u+v on lhs (u+v)^3 =−pz−q u^3 +3u^2 v+3uv^2 +v^3 =−pz−q 3uv(u+v)+u^3 +v^3 =−pz−q 3uvz+u^3 +v^3 =−pz−q by matching constants we get { ((I. uv=−(p/3) ⇔ u^3 v^3 =−(p^3 /(27)))),((II. u^3 +v^3 =−q)) :} (5) let u^3 =s and v^3 =t ⇒ { ((I. st=−(p^3 /(27)))),((II. s+t=−q)) :} this leads to a quadratic: I. ⇒ s=−(p^3 /(27t)); insert in II. ⇒ t−(p^3 /(27t))=−q ⇔ t^2 +qt−(p^3 /(27))=0 ⇒ ⇒ t=−(q/2)±(√((q^2 /4)+(p^3 /(27)))) ⇒ s=−(q/2)∓(√((q^2 /4)+(p^3 /(27)))) ⇒ we are free to choose the “+” value for t and the “−” value for s ⇒ u=((−(q/2)−(√((q^2 /4)+(p^3 /(27))))))^(1/3) and v=((−(q/2)+(√((q^2 /4)+(p^3 /(27))))))^(1/3) ⇒ z_1 =u+v z^3 +pz+q=(z−z_1 )(z^2 +(u+v)z+u^2 −uv+v^2 ) and we can solve this the only limitation is D=(q^2 /4)+(p^3 /(27))≥0 if D<0 we need the trigonometric solution
$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{Method} \\ $$$$\:\:\:\:\:{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{divide}\:\mathrm{by}\:{a}\:\Rightarrow \\ $$$$\:\:\:\:\:{x}^{\mathrm{3}} +\frac{{b}}{{a}}{x}^{\mathrm{2}} +\frac{{c}}{{a}}{x}+\frac{{d}}{{a}}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{let}\:{z}={x}−\frac{{b}}{\mathrm{3}{a}}\:\Rightarrow \\ $$$$\:\:\:\:\:{z}^{\mathrm{3}} +\frac{\mathrm{3}{ac}−{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }{z}+\frac{\mathrm{27}{a}^{\mathrm{2}} {d}−\mathrm{9}{abc}+\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{let}\:\frac{\mathrm{3}{ac}−{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }={p}\:\mathrm{and}\:\frac{\mathrm{27}{a}^{\mathrm{2}} {d}−\mathrm{9}{abc}+\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{27}{a}^{\mathrm{3}} }={q}\:\Rightarrow \\ $$$$\:\:\:\:\:{z}^{\mathrm{3}} +{pz}+{q}=\mathrm{0}\:\Leftrightarrow\:{z}^{\mathrm{3}} =−{pz}−{q} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{new}\:\mathrm{idea}:\:\mathrm{let}\:{z}={u}+{v}\:\mathrm{on}\:\mathrm{lhs} \\ $$$$\:\:\:\:\:\left({u}+{v}\right)^{\mathrm{3}} =−{pz}−{q} \\ $$$$\:\:\:\:\:{u}^{\mathrm{3}} +\mathrm{3}{u}^{\mathrm{2}} {v}+\mathrm{3}{uv}^{\mathrm{2}} +{v}^{\mathrm{3}} =−{pz}−{q} \\ $$$$\:\:\:\:\:\mathrm{3}{uv}\left({u}+{v}\right)+{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =−{pz}−{q} \\ $$$$\:\:\:\:\:\mathrm{3}{uvz}+{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =−{pz}−{q} \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{matching}\:\mathrm{constants}\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\:\:\:\:\begin{cases}{\mathrm{I}.\:\:{uv}=−\frac{{p}}{\mathrm{3}}\:\Leftrightarrow\:{u}^{\mathrm{3}} {v}^{\mathrm{3}} =−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\\{\mathrm{II}.\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =−{q}}\end{cases} \\ $$$$\left(\mathrm{5}\right)\:\mathrm{let}\:{u}^{\mathrm{3}} ={s}\:\mathrm{and}\:{v}^{\mathrm{3}} ={t}\:\Rightarrow \\ $$$$\:\:\:\:\:\begin{cases}{\mathrm{I}.\:\:{st}=−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\\{\mathrm{II}.\:{s}+{t}=−{q}}\end{cases} \\ $$$$\:\:\:\:\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{quadratic}: \\ $$$$\:\:\:\:\:\mathrm{I}.\:\Rightarrow\:{s}=−\frac{{p}^{\mathrm{3}} }{\mathrm{27}{t}};\:\mathrm{insert}\:\mathrm{in}\:\mathrm{II}.\:\Rightarrow \\ $$$$\:\:\:\:\:{t}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}{t}}=−{q}\:\Leftrightarrow\:{t}^{\mathrm{2}} +{qt}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}=\mathrm{0}\:\Rightarrow \\ $$$$\:\:\:\:\:\Rightarrow\:{t}=−\frac{{q}}{\mathrm{2}}\pm\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}} \\ $$$$\:\:\:\:\:\Rightarrow\:{s}=−\frac{{q}}{\mathrm{2}}\mp\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{we}\:\mathrm{are}\:\mathrm{free}\:\mathrm{to}\:\mathrm{choose}\:\mathrm{the}\:“+''\:\mathrm{value} \\ $$$$\:\:\:\:\:\mathrm{for}\:{t}\:\mathrm{and}\:\mathrm{the}\:“−''\:\mathrm{value}\:\mathrm{for}\:{s} \\ $$$$\:\:\:\:\:\Rightarrow\:{u}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}\:\mathrm{and}\:{v}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}} \\ $$$$\:\:\:\:\:\Rightarrow\:{z}_{\mathrm{1}} ={u}+{v} \\ $$$$\:\:\:\:\:\:\:\:\:\:{z}^{\mathrm{3}} +{pz}+{q}=\left({z}−{z}_{\mathrm{1}} \right)\left({z}^{\mathrm{2}} +\left({u}+{v}\right){z}+{u}^{\mathrm{2}} −{uv}+{v}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{limitation}\:\mathrm{is} \\ $$$${D}=\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}\geqslant\mathrm{0} \\ $$$$\mathrm{if}\:{D}<\mathrm{0}\:\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{solution} \\ $$
Answered by TANMAY PANACEA. last updated on 18/Apr/20
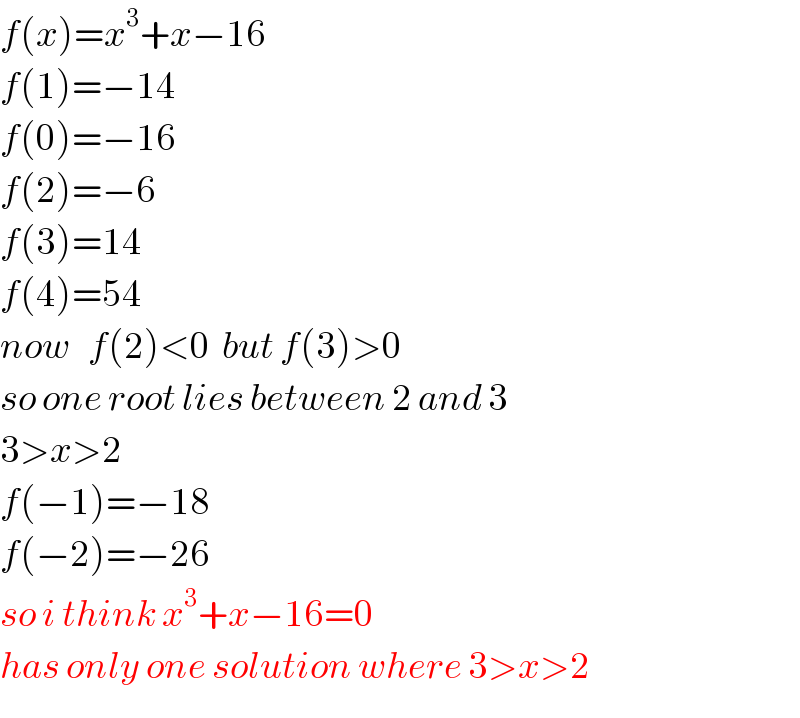
f(x)=x^3 +x−16 f(1)=−14 f(0)=−16 f(2)=−6 f(3)=14 f(4)=54 now f(2)<0 but f(3)>0 so one root lies between 2 and 3 3>x>2 f(−1)=−18 f(−2)=−26 so i think x^3 +x−16=0 has only one solution where 3>x>2
$${f}\left({x}\right)={x}^{\mathrm{3}} +{x}−\mathrm{16} \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{14} \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{16} \\ $$$${f}\left(\mathrm{2}\right)=−\mathrm{6} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{14} \\ $$$${f}\left(\mathrm{4}\right)=\mathrm{54} \\ $$$${now}\:\:\:{f}\left(\mathrm{2}\right)<\mathrm{0}\:\:{but}\:{f}\left(\mathrm{3}\right)>\mathrm{0} \\ $$$${so}\:{one}\:{root}\:{lies}\:{between}\:\mathrm{2}\:{and}\:\mathrm{3} \\ $$$$\mathrm{3}>{x}>\mathrm{2} \\ $$$${f}\left(−\mathrm{1}\right)=−\mathrm{18} \\ $$$${f}\left(−\mathrm{2}\right)=−\mathrm{26} \\ $$$${so}\:{i}\:{think}\:{x}^{\mathrm{3}} +{x}−\mathrm{16}=\mathrm{0} \\ $$$${has}\:{only}\:{one}\:{solution}\:{where}\:\mathrm{3}>{x}>\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *